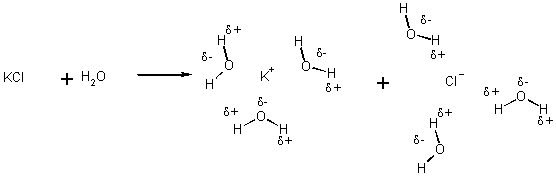
A solution is HOMOGENEOUS if we have just one phase present in a mixture of 2 or more substances
(Otherwise heterogeneous)
Why does dissolution occur?
- Entropy
- must balance intermolecular forces between different substances -
normally solvent and solute
solution
London forces for both
London London
dipole-dipole
H-bonding
ion-ion forces are overcome by
i) ion-dipole + entropy
But if crystal forces too strong, won't dissolve (AgCl / H2O),
KCl / EtOH, CuS/H2O
Do not dissolve in H2O or any solvent
E.g. C(diamond); SiC
Enthalpy of Solution
DHsoln may be positive or negative
e.g. CaCl2 DHsoln is negative (heat is liberated during dissolution)
lots of water (road salt)
Ammonium nitrate (NH4NO3) DHsoln is positive (heat is consumed from the environment during dissolution)
Entropy of solution!
[Demo
ROH + H2O
MeOH + H2O ® BuOH ok
pentanol + H2O no go
dipole << iodine
Demo Ammonium Nitrate
+ H2O (Temp)
(-oT) change
- negative enthalpy of solution
-KOH / H2O
(+ve T change) ]
Strong acids and bases fully ionized
Titrations
Equilibrium
Equilibrium constant expression
Weak acids AND Weak bases
e.g., Formic acid
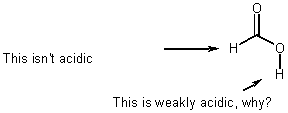
- equilibria (not rates)
H3O+
+ A_ (aq)
ie. Solution
Hydrogen Bond
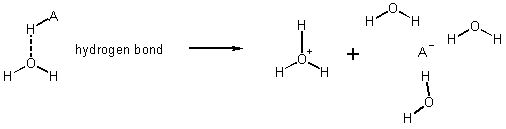
ie. Solution drive by solvation - water wants the H+ more than A- does.
e.g. HCl
What are strong acids? Compounds for which HO+H2 + A_ more stable than HA + H2O in solution
Typical examples of strong acids:HCl, HBr, HI, H2SO4, HNO3,
in water, all of these compounds completely dissolve AND completely dissociate.
e.g. HCl (g)+ H2O (l) 
H3O+ (aq) + Cl- (aq)
[H3O+] at equilibrium = [HCl] that was put into water
Kc = [H3O +] [Cl-] /[HCl][H2O] equilibrium constant
NaOH + H2O
Na+ (aq) + OH_ (aq)
NaNH2 + H2O
Na+ (aq) + NH3 + OH_ (aq)
NaCH3 + H2O
Na+ (aq)+ OH_ (aq) + CH4(g)
i.e. [OH-] at equilibrium = moles of NaOH dissolved/volume of solvent
i.e. [NaOH] init.
K = [Na+] [OH-] / [NaOH] [H2O]
as move right to left, harder to make anion
ease of anion generation, ie X- > OH_ > NH2_ > CH3_
ease of cation generation, X+ < +OR < +NR2 < +CR3
R = some atom or group
Due to electronegativity.
Where do the equilibria lie?
| 10-14 | HCl | + | H2O | |
H3O+ | + | OH- |
| 1014 | HOH | + | H2O | |
H3O+ | OH- | |
| 1035 | HNH2 | + | H2O | |
H3O+ | -NH2 | |
| 1050 | HCH3 | + | H2O | |
H3O+ | -CH3 |
H3O+ + OH-
Kc = [H3O+] [OH-] / [H2O] [H2O]
Kc [H2O]2 = [H3O+] [OH-]
= 1 x 10-14 (by conductivity measurements @ 25 oC )
[H2O] ~ 55M
1 L = 1000 g / 18g /mol
~ 55 M
Kc [H2O]2 = Kw = 1 x 10-14 = [H3O+] [OH-]
i.e. Water is a very weak acid
Take log of both sides
14 = pH + pOH
pH = - log [H3O+]
For pure water, what is pH?
Since [H3O+] = [OH-]
x = [H3O+]
x2 = 10-14
x = 10-7
- log x = 7
neutral pH = 7
pH + pOH = 14, therefore pOH = 7
| HCl | + | H2O | |
H3O+ | + | Cl- | |
| t=0 | 0.1M | 55M | - | - | |||
| t = infinity | - | 55 M | 0.1M | 0.1 M | |||
| eessentially no change |
If one had 0.3 mol of HCl in 1 L H2O, the pH = 3
Note: Only OH- + H+ contribute to pH, pOH not Cl-, Na+ etc. (counterions aren't important)
What about strong bases?
0.1 mol NaOH in 1L water
| NaOH | + | H2O | |
HO- | + | H3O+ | |
| t=0 | 0.1M | 55M | - | - | |||
| t = infinity | - | 55 M | 0.1M | 0.1 M | |||
| eessentially no change |
Kw = 1 x 10-14 = [H3O+] [OH-]
i.e. 14 = pH + pOH
pH = 14 - pOH
pH = 14 - 1 = 13
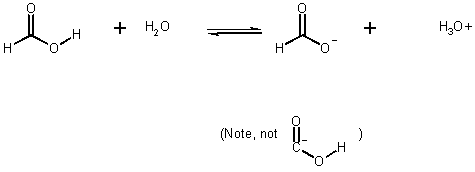
if 0.1 M in H2O, how much is dissociated?
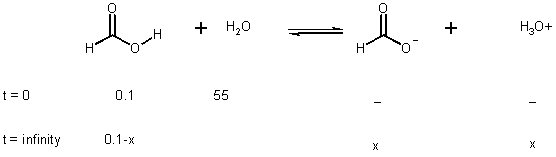
Kc =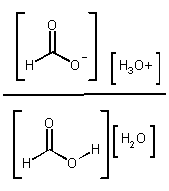 
OR
Kc [H2O] = Ka =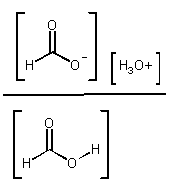 
Ka = acid dissociation constant
Ka = x2 / 0.1 - x
if assume x << 0.1 (5%)
x2 /0.1 - x = 1.8 x 10-4 (this comes from table on Page 802 and just above)
x2/0.1 = 1.8 x 10-4
x2 = 1.8 x 10-5
x= 4.2 x 10-3
x = [H3O+] pH = 2.37
(x at 4.2 x 10-3 is less than 5%, therefore this approximation is OK). Otherwise, you have to solve the quadratic.
for quadratic
ax2 + bx + c = 0 x2 + 1.8 x 10-4x - 1.8 x 10-5 = 0
x = 
= 
x = 4.3 x 10-3, that is, you get the same answer (<5%)
2) A weak base example
What is the OH- concentratioon in a 0.10 M solution of methylamine, CH3NH2? What is the percent dissociation of methylamine?
| CH3NH2 | + | H2O | |
HO- | + | CH3NH3+ | |
| t=0 | 0.1M | 55M | - | - | |||
| t = infinity | 0.1-x | - | x | x | |||
| essentially no change |
Kb = Keq [H2O] = [CH3NH3+] [OH-] / [CH3NH2]
(x)(x) / (0.10 - x) = 3.9 x 10-4 Kb for methylamine
x2 ~ (3.9 x 10-4) x 0.10
x ~ 6.2 x 10-3 mol L-1
% dissociation = 6.2 x 10-3 / 0.10 x 100 » 6%
Here we should not make approximation (we are over 5%)!!
Therefore solve quadratic
x2 / ( 0.10 - x) = 3.9 x 10-4
x2 + (3.9 x 10-4)x - 3.9 x 10-5 = 0
x = 
= 
x = .0060
% dissociation = 6.0 x 10-3 / .01 = 6% Since we did the quadratic, this the real value.
Another weak bases example
NH3 + H2O
NH4+ OH_
Keq = [NH4+] [OH-] / [H2O][NH3]
Kb = [NH4+] [OH-] / [NH3] = 1.8 x 10-5 (from the table)
if 0.02 M solution NH3
| CH3NH2 | + | H2O | |
HO- | + | NH4+ | |
| t=0 | 0.2M | 55M | - | - | |||
| t = infinity | 0.2-x | - | x | x | |||
| essentially no change |
assume
x << 0.02 (5%)
x2 = 1.8 x 10-5 x 0.02 = 3.6 x 10-7
x= 6.0 x 10-4
[OH-] = 6 x 10-4 pOH = 3.22 pH = 14 - 3.22 = 10.7
Check that x << .02
x=0.0006
=3%
Weak acid in water when we don't knowt he Ka
What about solution of NH4+ Cl in water
| NH4+Cl- | + | H2O | |
H3O+ | + | NH3 | |
| t=0 | 0.2M | 55M | - | - | |||
| t = infinity | 0.2-x | - | x | x | |||
| essentially no change |
Kb = 1.8 x 10-5 [OH-] [NH4+] / [NH3]
We need Ka for NH4+ - from where?
HA and H2O A-
+ H3O+
Ka = [H3O+] [A-] / [HA]
A- + H2O HO-
+ HA
Kb= [OH-] [HA] / [A-]
watch this
Kb (A-) x Ka (HA) = [H3O+] [OH-] = Kw
i.e. For any conjugate acid/base pair
Ka x Kb = Kw
pKa + pKb = 14 = pKw
i.e. If Kb = 1.8 x 10-5
pKb = 4.74
pKa = 14 - 4.74
= 9.26
Ka = 5.50 x 10-10
NOW WE CAN SOLVE THE PROBLEM OF NH4+ in water.
HNO3 + CH3-CO2H
CH3C+(OH)2 + -NO3
Such experiments show that:
HClO4 > H2SO4 > HNO3 > HCl
Acid strength of oxyacids depends on the number of oxygens. (We can write more canonical forms for the anion, and so delocalize the -ve charge)
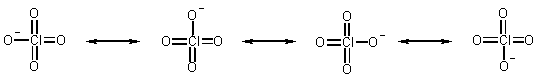
The perchlorate anion has 4 resonance forms (these are not four different rotamers, but 4 different ways in which the electrons can be shared over the 4 oxygen atoms).
ANOTHER EXAMPLE
pH of 0.1 M NaCN solution
CN- + H2O HCN
+ OH-
Kb = [HCN] [OH-] / [CN-]
= 2.0 x 10-5 (from table)
x2 / 0.1 (-x) = 2.0 x 10-5
x2 = 2.0 x 10-5 (x . 1)
x = 1.4 x 10-3
=.001 = less than 5% of .1
\ OK
x= 1.4 x 10-3 = [OH-]
pOH = 2.8 therefore pH = 11.2
Another example
e.g. find pH of 0.70 M solution of H4NCl (fully dissociated). 0.7 M NH4+ + 0.7 M Cl-
Kb (NH3) = 1.8 x 10-5
Eq- H4N+ + H2O
NH3 + H3O+
Ka= [H3O+] [NH3] / [NH4+] = 5.6 x 10-10
pH = 4.70
Ka= x2 / 0.7 - x
x2= 3.92 x 10-10
x=1.99 x 10-5
pH = [H3O+] = 4.7
[Demo
0.1 M CH3CO2- Na + HCl
CH3CO2- + H3O+
CH3CO2H + H2O
0.1M PhCO2Na + HCl
PHCO2- + HCl ® C6H5CO2H + H2O
0.1 M NaCO3 + HCl
CO32- + H3O- ® HCO3- + H2O
0.1 M NH4Cl + OH-
NH4+ + OH-
NH3 + H2O ]
Buffers contain
weak acid and conjugate base of weak acid (salt)
or
weak base + conjugate acid of weak base (salt)
Must use salts that are fully ionized
Two types of Buffers
i) weak base + conjugate acid of weak base
e.g.,
NaHCO3 + H3O+
H2CO3 + H2O
Base Conj acid
or
ii) Weak acid + conjugate base fo the weak acid
e.g. H4N+Cl_
+ OH- HOH + NH3
Acid Conj base
Let's do an example of a buffer solution, which has 100 mL of a solution that is
0.4 M PhCO2_ Na+
AND
0.5 M PhCO2H (C6H5COOH)
What is pH of this solution?
1. PhCO2- Na+ + H2O
Na PhCO2- (aq)
2. PhCO2H + H2O
H3O+ + PhCO2_
Ka = [H3O+][PhCO2_] / [PhCO2H] = 6.0 x 10-5 (from table)
| PhCO2H | + | H2O | |
H3O+ | + | PhCO2- | |
| t=0 | 0.5M | 55M | - | 0.4M | |||
| t = infinity | 0.5-x | - | x | 0.4 + x | |||
| essentially no change |
x = 6.0 x 10-5 x (0.50=/0.4) = 7.5 x 10-5 = [H3O+]
pH = -log (7.5 x 10-5) = 4.12
ie [H3O+] = Ka [PhCO2H] / [PhCO2_ ]
log each side
- log [H3O+] = -log Ka - log[PhCO2H] / [PhCO2_ ]
pH = pKa + log [PhCO2_ ] / PhCO2H]
Henderson - Hasselbalch equation. This is an equation YOU SHOULD REMEMBER
It applies if Ka of acid or Kb base < 10-3
pH = log 6.0 x 10-5 + log (.4/.5)
= 4.22 - .097 = 4.12
Adding a strong acid will remove some PhCO2_ from the equilibrium
PhCO2_ + H3O+
PhCO2H + H2O
We are adding HCl 10 mL x 10-3 L/mL x 0.15 mol/L = 1.5 x 10-3 mol
i.e.this removes 1.5 x 10-3 mol PhCO2_ and simultaneously produces 1.5 x 10-3 mol PhCO2H
New volume = 100 mL + 10 = 110
| PhCO2H | + | H2O | |
H3O+ | + | PhCO2- | |
| t=0 | (50 x 10-3 mol + 1.5 x 10-3 mol )/ 110 x 10-3L | 55M | - | (40 x 10-3 mol - 1.5 x 10-3 mol) / 110 x 10-3L | |||
| t = infinity | (51.5 x 10-3-x)/110 x 10-3L | - | x | (38.5 x 10-3 + x )/110 x 10-3L | |||
| essentially no change |
Ka = 6.0 x 10-5 = x (38.5/110 + x) / (51/110 - x) (again assume x << 38.5/110)
x= 8.02(6) x 10-5 = [H3O+] pH=4.10 (compare 4.12)
i.e., we added some strong acid to the solution, but the pH only changed a small amount - the solution was buffered.
The easier way to calculate this is to use the Henderson Hasselbalch Equation
pH = pKa + log [PhCO2-] / [PhCO2H]
[PhCO2H]= 0.100 L x 0.5 mol/L + 0.01L x .15 mol/L / .110 L
= .05 + .0015 mol / .11 L
= .0515 mol / .11 L = .468 M
[PhCO2-]= .100 L x 0.4 mol/L + 0.01L x .15 mol/L / .110 L
= .04 + .0015 mol / .11 L
= .0385 mol / .11 L = .35M
[PhCO2-] / [PhCO2H] = 1.338
log = 1.13
pH = pKa - 0.13 = 4.22 -0.13 = 4.09 compare 4.12
[Demo Buffering
H2O + 0.01 M NaOH
0.01 M HCl
Blood Plasma ]
Molarity H3O+ = 0.15 M x 0.01 L = 1.5 X 10-3 moles
Volume = 100 + 10 = 0.11 L
[H3O+] = 1.5 x 10-3 mol / 0.11 L
[H3O+] = 1.36 x 10-2
pH = 1.86
Much more acidic when not buffered!
1) KOH + PhCO2H
PhCO2_ + H2O
2) PhCO2H + H2O H3O+
+ PhCO2-
as before pH = 4.14
If 10 mL 0.15 M KOH in buffer
PhCO2H + H2O
H3O+ + PhCO2_
AS ABOVE
pH = pKa + log (42.5 x 10-3 / 47.5 x 10-3)
pH = 4.17
or more likely
loses a proton to become negatively charged
HIn + H2O H3O+
+ In_
e.g., Anthocyanidins flowers, sweet cherries
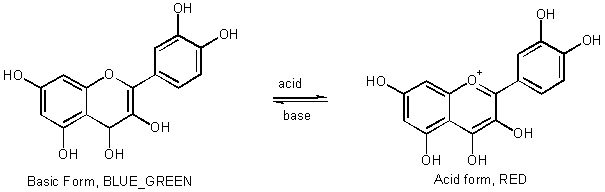
[Demo Indicators
(Can we do wine changing)
or
1) Indicator pH of a 1:1 In_ / HIn mixture
i) bromophenol ~ 5
ii) Methyl red 4 - 5
iii) Bromothymol Blue 7
iv) Phenolphtalein 8, 9, 10
2) Natural Indicators
i) MeOH extract Begonia blooms
ii) grape juice]
HIn + H2O H3O+
+ In_
RED
BLUE-GREEN
Acid Form
Base Form
pH
RED £ 4 - 6 £
yellow
Orange
In order to really be sure of the colour, need at least a 10 fold excess of one form
ie. Ratio [In_]/[HIn] » 10/1 to see the blue-green colour
for an indicator with a pKa = 5
pH = pKa + log [In-] / [HIn]
For [In-] / [Hin] = 1/1 pH= pKa + 0 = 5 (log 1)
but to see red (for sure!) in acid
Ratio [In-] / [HIn] = 1/10
pH = 5 + log (1/10) = 5 - 1 = 4
To see blue-green in base
Ratio [In-] / [HIn] = 10/1
pH = 5 + log (10/1) = 5 + 1 = 6
| Indicator | pH Range | Colour Change | pKa |
| Methyl Violet | 0-3 | yellow-violet | 1.6 |
| Methyl Orange | 3.3-4.6 | red-yellow | 4.2 |
| Methyl Red | 4.2-6.2 | Red-yellow | 5.2 |
| Bromthymol Blue | 6.0-7.8 | Yellow-Blue | 7.1 |
| Thymol Blue | 6.9-9.4 | Yellow-Blue | 8.2 |
| Phenolphthalein | 8.3-10.0 | Colourless-Red | 9.5 |
| Alizarine Yellow | 10.1-12.1 | Yellow-Red | 11.0 |
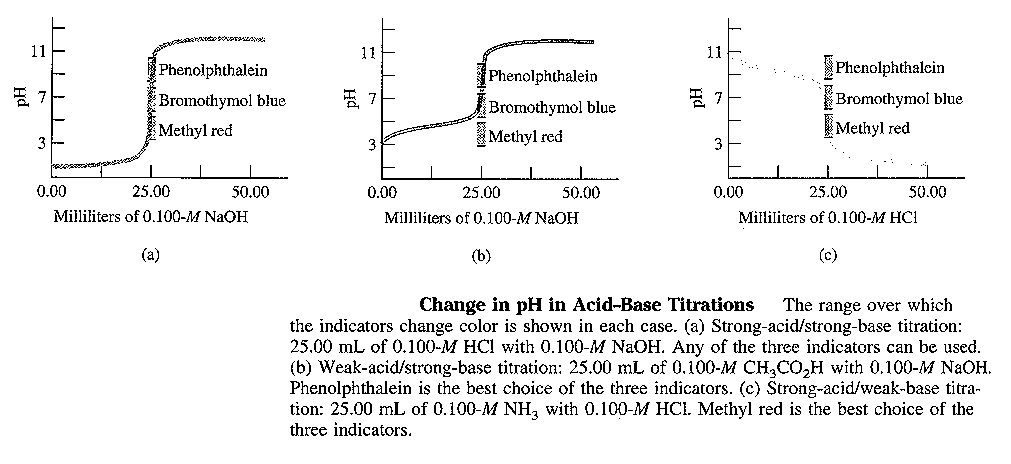
Strong acid + Strong Base
water + salt
e.g., take 50.0 mL of 0.10 M HCl titrateed with 0.10 M HCl
| base added (mL) | pH |
| 0 | 1 |
| 10 | 1.18 |
| 20 | 1.37 |
| 40 | 1.95 |
| 45 | 2.28 |
| 48 | 2.69 |
| 49 | 3.0 |
| 50 | 7.0 |
| 51 | 11.0 |
| 55 | 11.68 |
| 60 | 11.96 |
| 80 | 12.36 |
| 100 | 12.52 |
| large excess | 13 |
Titrate with: 100 mL 0.1 M KOH
x = 1.34 x 10-3 pH = 2.87
[OH-] = 100 mL x 0.1 M
= 10 mmol NaOH/-
@ equivalence point = 0.05 M NaOAc
CH3CO2Na + H2O
OH- + H3CCO2H
0.05 - x x x
x2 / 0.05 = Kb = 1 x 10-14 / 1.8 x 10-5 (Kw/Ka)
x2=2.7 x 10-11
x= 5.3 x 10-6 pOH 5.27 pH = 8.72
pH = 4.74 + log [0.005/150 mL]/[0.005/150 mL]
= 4.74
pH = 4.74 + log [0.0025/125 mL]/[0.075/125 mL]
= 4.74 + log [0.0025]/[0.075]
=4.26