CHEMISTRY 1AA3, TUTORIAL PROBLEM SET 5A

Week of March 15, 1999 - ANSWERS

________________________________________________________________________________
1. Draw line structures and name 5 of the structural isomers of molecular formula C₅H₁₁Cl.

A) 1-chloropentane, B) 2-chloropentane, C) 3-chloropentane, D) 1-chloro-3-methylbutane, E) 2-chloro-3-methylbutane, F) 2-chloro-2-methylbutane, G) 1-chloro-2,2-dimethylpropane, H) 1-chloro-2-methylbutane,

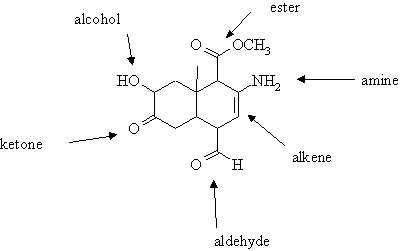
2. Name all the functional groups in the following molecule.

3. Write Lewis structures for the following: i) CH₃O₂CH₃ ii) HCO₂CH₃ iii) BrCHCH₃CH₂Cl iv) CH₃COC₂H₅ v) CH₃CHNOH

4. Write out the structural formulas for the following molecules. i) 2-amino-1-hydroxybutane ii) cis-1-chloro-3-methylcyclopentane iii) 2-bromo-3-chloro-3-methylhexane

5. Determine the E or Z geometric configurations for the following alkenes and name them.
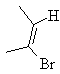i)

ii)

iii)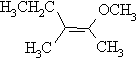

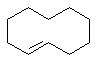
E-cyclodecane E-2-bromobut-2-ene Z-2-methoxy-3-methylpent-2-ene

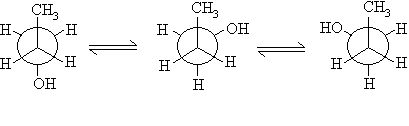
6. Draw Newman projections for 1-propanol looking along the C1-C2 bond. Label each conformer as anti or gauche. Which of these three would you expect to be the most stable.

anti gauche gauche

The anti is more stable.

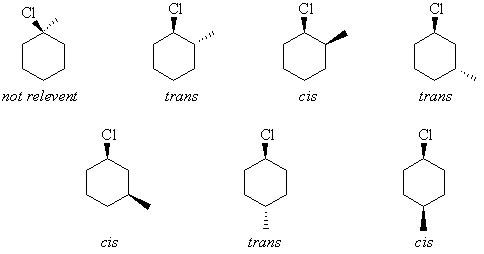
7. Write out all the structural and geometric isomers (stereoisomers) of chloromethylcyclohexane. Use planar projections formulae and indicate the orientation (stereochemistry) of the Cl and Me groups by using a wedged line (out of the plane of the page) and dashed line (below the plane of the page). Label each of the isomers are cis or trans.

8. The free-radical chlorination of pentane gives a mixture of 3 monochloropentanes. Assume the statistical differences in numbers of H’s relate linearly to the product produced

i) Draw their structures

ii) give their names

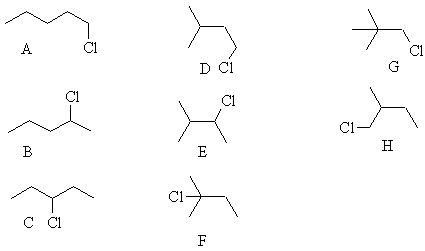
1-chloropentane 2-chloropentane 3-chloropentane

iii) predict the ratios of the three products remembering that a chlorine abstracts a secondary H (CH₂) about 4 times faster than a primary H (CH₃).

You need to consider the statistical number of hydrogens and the relative rate with which they will react. We know k₁ =k₂ /4

The free radical chlorination of alkanes involves 3 steps.

Initiation: Cl₂ ® 2 Cl

Prop HCR₃ + Cl® HCl + HCR₂

HC R₂+ Cl₂® HCR₂Cl + Cl

Term Cl+ Cl®Cl₂

Cl+ HCR₂®HCR₂ Cl

HCR₂+ HCR₂+ ® HCR₂CR₂H

The important question is whether CH₂ of CH₃ is more reactive. We learned that a 2^o radical is more stable than a 1^o radical. Also important is the statistical differences between 2 x CH₃ group, 2 x CH₂ groups (C2), and 1 x CH₂ groups (C3)

But k₁ = k₂ / 4 and there is the statistical difference in the numbers of hydrogens present to react.

(6H for the Me groups versus 4H for the (C2) CH₂ groups and 2H for the (C3) CH₂).

Rate producing 1-chloropentane = k₁ [pentane] * number of primary hydrogens

Rate producing 2-chloropenane = k₂ [pentane] * number of secondary hydrogens on C2

Rate producing 3-chloropenane = k₂ [pentane] * number of secondary hydrogens on C3

Fraction that reacts to give 1-chloropentane = k₁ *6

Fraction that reacts to give 2-chloropentane = k₁ * 4 *4

Fraction that reacts to give 3-chloropentane = k₁ * 4 *2

sum of fractions = 1 (all pentane reacts to give a monochloropentane)

1 = k₁ *6 + k₁ * 4 *4 + k₁ * 4 *2 k₁= 1/(6+16+8) = = 1/30 = 0.033

Therefore amount of 1-chloropentane = k₁ *6 = 0.033 * 6 = 20%

Therefore amount of 2-chloropentane = k₁ * 4.5 *4 = 0.033 * 16 = 53%

Therefore amount of 2-chloropentane = k₁ * 4 *2 = 0.033 * 8 = 26%