![[Envelope of Electron Density for Ethene]](./f2b-201.gif)
|
Matter is composed of atoms. This is a consequence of the manner in which the electrons are distributed throughout space in the attractive field exerted by the nuclei. The nuclei act as point attractors immersed in a cloud of negative charge, the electron density 
(r). The electron density describes the manner in which the electronic charge is distributed throughout real space. The electron density is a measurable property and it determines the appearance and form of matter. This is illustrated in the following figures. Figure 1 displays the spatial distribution of the electron density in the plane containing the two carbon and four hydrogen nuclei of the ethene molecule. The electron density is a maximum at the position of each nucleus and decays rapidly away from these positions. When this diagram is translated into three dimensions, the cloud of negative charge is seen to be most dense at nuclear positions and to become more diffuse as one moves away from these centres of attraction, as illustrated in Figure 2. The presence of local maxima at the positions of the nuclei is the general and also the dominant topological property of (r). Figure 3 illustrates the same feature for the 110 plane of carbon nuclei in the diamond lattice.
Figure 1. (a) The electron density in the plane containing the two carbon and four hydrogen nuclei of the ethene molecule, portrayed as a projection in the third dimension and in the form of a contour map. The absolute maxima in
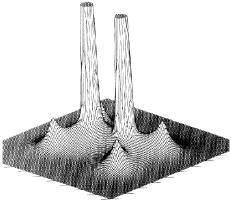
Figure 1. (b) Same as in Figure 1a, but for a plane obtained by a rotation of 90° about the C-C axis, a plane containing only the carbon nuclei.
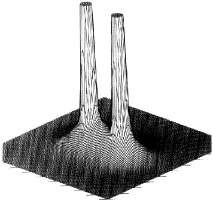
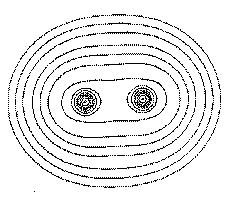
Figure 1. (c) Again, the same portrayal as in Figure 1a, but this time for a plane perpendicular to the C-C axis at its mid-point. What appears as a C-C saddle in (a) is seen to be a maximum in the plane perpendicular to the C-C axis. The point exhibits two negative curvatures perpendicular to this axis and one positive curvature along the axis.
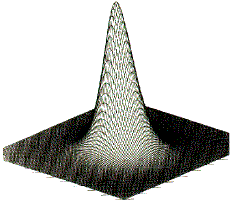
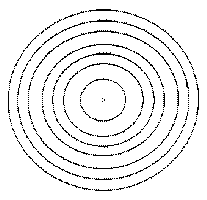
Figure 2. Envelopes of the electron density for the ethene molecule for values (in atomic units) of 0.002 in (a), 0.20 in (b) and 0.36 in (c). Matter consists of point-like nuclei embedded in a spatial distribution of negative charge that becomes increasingly diffuse for points progressively removed from the nuclei.
Figure 3. The electron density for diamond as projection above a 110 plane. The second diagram displays the tetrahedral structure of the bond paths linking the carbon nuclei in diamond, lines that are a consequence of the topology exhibited by the electron density.
To determine what physics has to say about this property of the electron density one must consider not the density itself but the field one obtains by following the trajectories traced out by the gradient vectors of the density. Starting at any point, one determines the gradient of
(r). This is a vector that points in the direction of maximum increase in the density. One makes an infinitesimal step in this direction and then recalculates the gradient to obtain the new direction. By continued repetition of this process, one traces out a trajectory of 
(r).
A gradient vector map generated in this manner is illustrated in the upper diagram of Figure 4 for the same plane of the ethene molecule shown in Figure 1. Since the density exhibits a maximum at the position of each nucleus, sets of trajectories terminate at each nucleus. The nuclei are the attractors of the gradient vector field of the electron density. Because of this fundamental property, the space of the molecule is disjointly and exhaustively partitioned into basins, a basin being the region of space traversed by the trajectories terminating at a given nucleus or attractor. Since a single attractor is associated with each basin, an atom is defined as the union of an attractor and its basin.
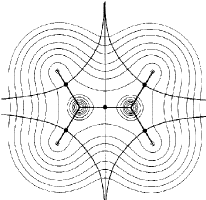
Figure 4. Maps of the gradient vector field of the electron density for the same plane containing the nuclei shown in Figure 1. Each line represents a trajectory traced out by the vector
Figure 4. (a) A display of the trajectories that terminate at the nuclei. Each trajectory is arbitrarily terminated at the surface of a small circle centered on the nucleus. The set of trajectories that terminate at a given nucleus (attractor) cover the basin of the attractor. |
|
Figure 4. (b) The same as (a) but including the sets of trajectories which terminate and originate at the bond critical points (denoted by dots). Only one pair of an (infinite) set of trajectories that terminate at the critical point lie in this plane. |
|
Figure 4. (c) A contour map of the electron density overlaid with the bond paths that define the molecular graph and with the trajectories that mark the intersection of the interatomic surfaces with this plane and define the boundaries of the atomic basins. |
|
Next Section: What is a Bond?
Previous Section: Introduction
| Go to: |
R.F.W. Bader Research Group AIMPAC and Other AIM Software Department of Chemistry Faculty Department of Chemistry Welcome Page McMaster University Welcome Page |
02dec97; rfwb
