![[Carbon Hydride: Interatomic Surface]](./f8c-201.gif)
- Introduction
- What is an Atom?
- What is a Bond?
- The Topological Atom is the Quantum Atom
- Quantum Mechanics of a Proper Open System
- The Laplacian of the Electron Density and the Lewis and VSEPR Models
- Further Reading

![[Carbon Hydride: Interatomic Surface]](./f8c-201.gif) |
|
The Topological Atom is the Quantum Atom
 The definition of an atom in terms of the topology of the electron density is neither valid nor useful if its properties are not predicted by quantum mechanics. The fundamental nature of the atom, as the building block of matter, follows from the demonstration that the topological and quantum definitions of an atom coincide. An atom can be alternatively defined as a region of real space bounded by surfaces through which there is a zero flux in the gradient vector field of the electron density. This is clear from Figure 5, which shows that an interatomic surface is defined by the set of trajectories that terminate at a point where
The definition of an atom in terms of the topology of the electron density is neither valid nor useful if its properties are not predicted by quantum mechanics. The fundamental nature of the atom, as the building block of matter, follows from the demonstration that the topological and quantum definitions of an atom coincide. An atom can be alternatively defined as a region of real space bounded by surfaces through which there is a zero flux in the gradient vector field of the electron density. This is clear from Figure 5, which shows that an interatomic surface is defined by the set of trajectories that terminate at a point where ![]()
![]() (r) = 0. Thus an interatomic surface satisfies the "zero-flux" boundary condition stated in equation (1)
(r) = 0. Thus an interatomic surface satisfies the "zero-flux" boundary condition stated in equation (1)
where n(rs) is the unit vector normal to the surface at rs. In words, the surface is not crossed by any trajectories of ![]()
![]() (r). An atom, as a constituent of some larger system, is itself an open system subject to fluxes in charge and momentum through its bounding surface.
(r). An atom, as a constituent of some larger system, is itself an open system subject to fluxes in charge and momentum through its bounding surface.
 Around 1950, Feynman and Schwinger, following along a path first traversed by Dirac, developed a new formulation of quantum mechanics based upon the classical principle of least action. Their work enables one to ask and answer questions that could not be answered using the Hamiltonian-based approach to quantum mechanics.
Schwinger's generalization of the action principle, as contained in his principle of stationary action, in addition to determining the field equation, yields a variational derivation of Heisenberg's equation of motion for any observable
Around 1950, Feynman and Schwinger, following along a path first traversed by Dirac, developed a new formulation of quantum mechanics based upon the classical principle of least action. Their work enables one to ask and answer questions that could not be answered using the Hamiltonian-based approach to quantum mechanics.
Schwinger's generalization of the action principle, as contained in his principle of stationary action, in addition to determining the field equation, yields a variational derivation of Heisenberg's equation of motion for any observable  . This principle equates the change in action to the infinitesimal (
. This principle equates the change in action to the infinitesimal (![]() ) transformations caused by the generators -(i
) transformations caused by the generators -(i![]() /
/![]() )
)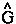 acting in the space-like and time-like surfaces that bound the space-time volume swept out by a system, as well as to displacements in these surfaces.
A time-like surface describes the temporal evolution of the spatial boundary enclosing a portion of some total system. Thus Schwinger's principle enables one to derive a quantum description of an open system. In doing so one obtains the remarkable result that only an open system bounded by surfaces satisfying the `zero-flux' boundary condition stated in equation (1) yields an expression for the change in action that is the same in form and content to that for an isolated system and in addition, yields equations of motion for the observables that are identical to those predicted by the field equation. Thus the definition of an open system at the atomic level is not open to choice but is determined by physics. Consequently, an open system satisfying equation (1) is termed a proper open system.
acting in the space-like and time-like surfaces that bound the space-time volume swept out by a system, as well as to displacements in these surfaces.
A time-like surface describes the temporal evolution of the spatial boundary enclosing a portion of some total system. Thus Schwinger's principle enables one to derive a quantum description of an open system. In doing so one obtains the remarkable result that only an open system bounded by surfaces satisfying the `zero-flux' boundary condition stated in equation (1) yields an expression for the change in action that is the same in form and content to that for an isolated system and in addition, yields equations of motion for the observables that are identical to those predicted by the field equation. Thus the definition of an open system at the atomic level is not open to choice but is determined by physics. Consequently, an open system satisfying equation (1) is termed a proper open system.
 A total isolated system also satisfies equation (1). Thus a single principle of physics determines the properties of the total system and its constituent atoms. The properties of the topological atoms coincide with those ascribed to the atoms of chemistry; (i) they are additive to yield the corresponding property for the total system and (ii) they are transferable from one system to another to the extent that the transfer leaves their distribution of charge unchanged.
It is known from experiment that atoms and functional groupings of atoms can be transferable to a remarkable degree and that when this occurs, one can determine the atomic or group contributions to the total properties of a system. The theory of atoms in molecules recovers the experimentally determined characteristic and additive group contributions to all properties, as has been demonstrated for the volume, energy, electric polarizability and magnetic susceptibility. These are the atoms of chemistry.
A total isolated system also satisfies equation (1). Thus a single principle of physics determines the properties of the total system and its constituent atoms. The properties of the topological atoms coincide with those ascribed to the atoms of chemistry; (i) they are additive to yield the corresponding property for the total system and (ii) they are transferable from one system to another to the extent that the transfer leaves their distribution of charge unchanged.
It is known from experiment that atoms and functional groupings of atoms can be transferable to a remarkable degree and that when this occurs, one can determine the atomic or group contributions to the total properties of a system. The theory of atoms in molecules recovers the experimentally determined characteristic and additive group contributions to all properties, as has been demonstrated for the volume, energy, electric polarizability and magnetic susceptibility. These are the atoms of chemistry.
 The envelope of the electron density, of value 0.001 atomic units, contains almost all of the electronic charge of a system and provides a measure of its van der Waals size and shape. The intersection of the interatomic surfaces of an atom or a group with this envelope thus yields a display of the group as a space-filling object, examples of which are shown in Figures 8 and 9. All proper open systems are transferable to some extent, this property underlying the usefulness of the atomic model in chemistry.
The envelope of the electron density, of value 0.001 atomic units, contains almost all of the electronic charge of a system and provides a measure of its van der Waals size and shape. The intersection of the interatomic surfaces of an atom or a group with this envelope thus yields a display of the group as a space-filling object, examples of which are shown in Figures 8 and 9. All proper open systems are transferable to some extent, this property underlying the usefulness of the atomic model in chemistry.
Figure 8. Depictions of atoms and functional groupings of atoms as space-filling objects - regions bounded by the intersection of the interatomic surfaces and the van der Waals envelope of the electron density. The second-row hydrides AHn where A = Li, Be, B, C, N, O and F. Note the change in the size and form of the hydrogen atom, from one characteristic of the hydride ion in LiH to the positively charged one in HF, wherein the atom has been stripped of more than half of its electron density.

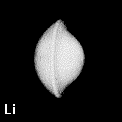


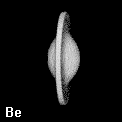


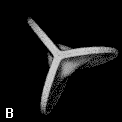
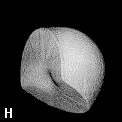


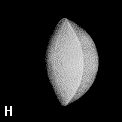


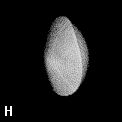


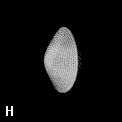


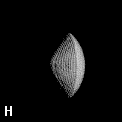

Figure 9. (a) The transferable methyl group of the normal hydrocarbons. This group remains essentially unchanged throughout this series of molecules and contributes a fixed amount to each property, including the volume, energy, electric polarizability and magnetic susceptibility. (b) The alanyl peptide unit bounded by its two amidic interatomic surfaces. This group, like all groups that serve as transferable building blocks, has a zero net charge and a fixed set of properties.
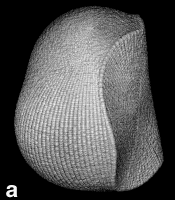

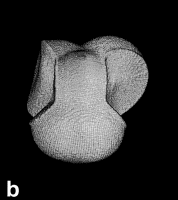
Next Section: Quantum Mechanics of a Proper Open System
Previous Section: What is a Bond?
| Go to: |
R.F.W. Bader Research Group AIMPAC and Other AIM Software Department of Chemistry Faculty Department of Chemistry Welcome Page McMaster University Welcome Page |
02dec97; rfwb