![[Current Trajectories in Carbon Dioxide]](./f10-201.gif)
- Introduction
- What is an Atom?
- What is a Bond?
- The Topological Atom is the Quantum Atom
- Quantum Mechanics of a Proper Open System
- The Laplacian of the Electron Density and the Lewis and VSEPR Models
- Further Reading

![[Current Trajectories in Carbon Dioxide]](./f10-201.gif) |
|
Quantum Mechanics of a Proper Open System
 There is no such thing as an isolated system, and all systems are open systems that experience varying degrees of interaction through their shared zero-flux surfaces. Thus the statement of the principle of stationary action for a proper open system is simply a generalization of quantum mechanics that applies to all physical systems. The operational statement of this theory is most elegantly and simply stated using the language of field theory. The principle, when stated in terms of a variation of the Lagrange-function operator
There is no such thing as an isolated system, and all systems are open systems that experience varying degrees of interaction through their shared zero-flux surfaces. Thus the statement of the principle of stationary action for a proper open system is simply a generalization of quantum mechanics that applies to all physical systems. The operational statement of this theory is most elegantly and simply stated using the language of field theory. The principle, when stated in terms of a variation of the Lagrange-function operator 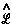 [
[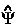 ,t,
,t,![]() ] for the observable
] for the observable 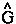 , and in a form that is applicable to any region of space
, and in a form that is applicable to any region of space ![]() bounded by a zero-flux surface, is
bounded by a zero-flux surface, is
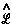 [
[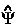 ,t,
,t,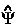 |[
|[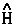 ,
,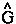 ]|
]|
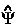 >
>
The observable 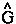 multiplied by -(i
multiplied by -(i![]() /
/![]() ), where
), where ![]() denotes a real infinitesimal, is the generator of a corresponding unitary transformation in the Lagrange-function and one sees that Schwinger's principle combines the action principle with Dirac's transformation theory. The variation in
denotes a real infinitesimal, is the generator of a corresponding unitary transformation in the Lagrange-function and one sees that Schwinger's principle combines the action principle with Dirac's transformation theory. The variation in 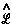 [
[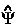 ,t,
,t,![]() ] may be alternatively expressed as
] may be alternatively expressed as
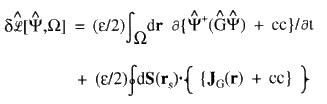 (3)
(3)
that is, by the time rate-of-change of the property density for G together with a term accounting for the flux in JG(r), the vector current of this density, through the surface S(rs) bounding the region ![]() . This latter term vanishes for an isolated system.
. This latter term vanishes for an isolated system.
 The Table below lists the atomic theorems obtained using equation (2) for a number of important generators. The Schrödinger representation is used in these equations and the expression
The Table below lists the atomic theorems obtained using equation (2) for a number of important generators. The Schrödinger representation is used in these equations and the expression ![]() d
d![]() ' denotes a summation over all spins and an integration over the spatial coordinates of all electrons but the one whose coordinates appear in the observable
' denotes a summation over all spins and an integration over the spatial coordinates of all electrons but the one whose coordinates appear in the observable 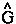 .
.
| Atomic Theorems |
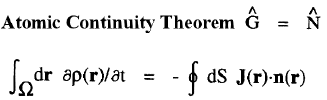 |
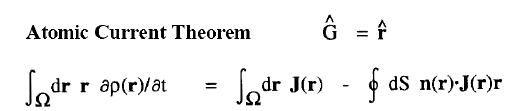 |
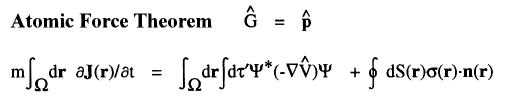 |
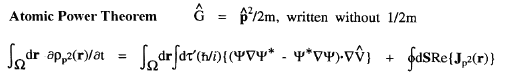 |
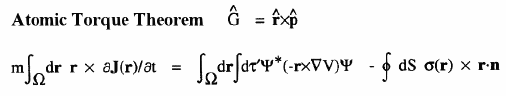 |
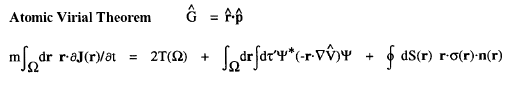 |
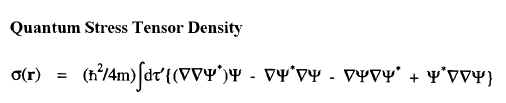 |
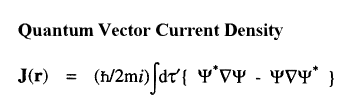 |
For example, the time rate-of-change of momentum is force and when  =
=  , one obtains the Ehrenfest atomic force theorem. In this case [
, one obtains the Ehrenfest atomic force theorem. In this case [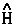 ,
,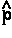 ] = i
] = i![]()
![]()
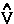 , where
, where 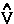 is the total potential energy operator.
The vector current J(r) is the momentum density divided by the mass of the electron m and the integral of its time rate-of-change multiplied by m yields the force acting on the atom. This force is equated to the sum of a basin and a surface contribution: the basin contribution is the commutator average and the surface term is the momentum flux through the surface, a term described by the quantum stress tensor
is the total potential energy operator.
The vector current J(r) is the momentum density divided by the mass of the electron m and the integral of its time rate-of-change multiplied by m yields the force acting on the atom. This force is equated to the sum of a basin and a surface contribution: the basin contribution is the commutator average and the surface term is the momentum flux through the surface, a term described by the quantum stress tensor ![]() (r). In a stationary state, the basin term for a given
(r). In a stationary state, the basin term for a given 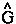 is balanced by its surface flux contribution.
is balanced by its surface flux contribution.
The ![]() d
d![]() ' averaging of the commutator yields the force exerted on an electron at a point r in
' averaging of the commutator yields the force exerted on an electron at a point r in ![]() , as determined by averaging over the motions of all the remaining particles in the system. Thus it describes a force density and its integral over
, as determined by averaging over the motions of all the remaining particles in the system. Thus it describes a force density and its integral over ![]() yields the average force exerted on the basin of the atom. The basin contributions to all properties are determined by a corresponding property density. Thus when
yields the average force exerted on the basin of the atom. The basin contributions to all properties are determined by a corresponding property density. Thus when 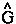 =
= 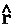 ·
·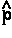 the commutator yields -
the commutator yields -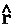 ·
·![]()
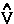 whose
whose ![]() d
d![]() ' averaging yields the electronic potential energy density. This density expresses in a rigorous manner, the local potential energy experienced by a single electron determined in the average field of all the remaining particles in a many-particle system.
The kinetic energy T(
' averaging yields the electronic potential energy density. This density expresses in a rigorous manner, the local potential energy experienced by a single electron determined in the average field of all the remaining particles in a many-particle system.
The kinetic energy T(![]() ) and the potential energy defined by the atomic virial theorem have the remarkable and necessary property that they are as transferable as is the electron density. Proper open systems are the most transferable pieces of matter one can define in an exhaustive partitioning of the real space of any system, leading to their most important property; if the distribution of electronic charge is essentially unchanged for a given atom in two different systems, then its properties, including its energy, are transferable as well as additive, the atom contributing the same amounts to all properties in both systems. It is the energy defined by the atomic virial theorem that exhibits the essential physical requirement that two identical pieces of matter possess identical energies, be they of macroscopic or microscopic dimensions, in the form of equivalent atoms at different sites within a crystal or two identical peptide units in a polypeptide.
) and the potential energy defined by the atomic virial theorem have the remarkable and necessary property that they are as transferable as is the electron density. Proper open systems are the most transferable pieces of matter one can define in an exhaustive partitioning of the real space of any system, leading to their most important property; if the distribution of electronic charge is essentially unchanged for a given atom in two different systems, then its properties, including its energy, are transferable as well as additive, the atom contributing the same amounts to all properties in both systems. It is the energy defined by the atomic virial theorem that exhibits the essential physical requirement that two identical pieces of matter possess identical energies, be they of macroscopic or microscopic dimensions, in the form of equivalent atoms at different sites within a crystal or two identical peptide units in a polypeptide.
 When a molecule is placed in a uniform external magnetic field, a flow of electric current is induced within the molecule. This current is described by the quantum current density J(r) introduced above and appearing in the atomic current theorem. This theorem states that the atomic average of J(r), the average velocity of the electrons within the atom as induced by the applied field, is equal to the flux through its atomic surface of the tensor corresponding to the position weighted current.
Because of this theorem, the magnetic susceptibility of a molecule can be equated to a sum of atomic or group contributions and the values so defined recover Pascal's experimentally determined values for the corresponding group increments for the hydrocarbons. The same current determines the shielding or deshielding of a nucleus from the applied magnetic field in an NMR experiment, and this shielding is also expressible as a sum of atomic contributions; see references 6 and 7.
When a molecule is placed in a uniform external magnetic field, a flow of electric current is induced within the molecule. This current is described by the quantum current density J(r) introduced above and appearing in the atomic current theorem. This theorem states that the atomic average of J(r), the average velocity of the electrons within the atom as induced by the applied field, is equal to the flux through its atomic surface of the tensor corresponding to the position weighted current.
Because of this theorem, the magnetic susceptibility of a molecule can be equated to a sum of atomic or group contributions and the values so defined recover Pascal's experimentally determined values for the corresponding group increments for the hydrocarbons. The same current determines the shielding or deshielding of a nucleus from the applied magnetic field in an NMR experiment, and this shielding is also expressible as a sum of atomic contributions; see references 6 and 7.
Figure 10. Display of the trajectories of the current induced in the carbon dioxide molecule by a magnetic field directed out of the plane of the diagram. The interatomic surfaces separating the basins of the carbon and oxygen atoms are also indicated. Note how these surfaces isolate the paramanegtic current flow in the basin of the carbon atom.

 Figure 10 illustrates the current induced in the carbon dioxide molecule for a magnetic field directed out of the plane of the diagram. This display of the calculated current is made possible through the use of the theory of atoms in molecules in overcoming the "gauge origin" problem. One sees the presence of both diamagnetic (clockwise) and paramagnetic (counter-clockwise) currents with the former dominating. The current induced by an externally applied magnetic field determines all of the magnetic response properties exhibited by a molecule and understanding these properties requires an understanding of the induced current and its atomic contributions. Thus the presence of the paramagnetic currents within the basin of the carbon atom in carbon dioxide provides a clear physical explanation of the magnetic susceptibility and the magnetic shielding of the nuclei in this molecule.
Figure 10 illustrates the current induced in the carbon dioxide molecule for a magnetic field directed out of the plane of the diagram. This display of the calculated current is made possible through the use of the theory of atoms in molecules in overcoming the "gauge origin" problem. One sees the presence of both diamagnetic (clockwise) and paramagnetic (counter-clockwise) currents with the former dominating. The current induced by an externally applied magnetic field determines all of the magnetic response properties exhibited by a molecule and understanding these properties requires an understanding of the induced current and its atomic contributions. Thus the presence of the paramagnetic currents within the basin of the carbon atom in carbon dioxide provides a clear physical explanation of the magnetic susceptibility and the magnetic shielding of the nuclei in this molecule.
Final Section: The Laplacian of the Electron Density and the Lewis and VSEPR Models
Previous Section: The Topological Atom is the Quantum Atom
| Go to: |
R.F.W. Bader Research Group AIMPAC and Other AIM Software Department of Chemistry Faculty Department of Chemistry Welcome Page McMaster University Welcome Page |
02dec97; rfwb