An Introduction to the Electronic Structure of Atoms and Molecules

With our knowledge of the electronic structure of atoms we are now in a position to understand the existence of molecules. Clearly, the force which binds the atoms together to form a molecule will, as in the atomic case, be the electrostatic force of attraction between the nuclei and electrons. In a molecule, however, we encounter a force of repulsion between the nuclei in addition to that between the electrons. To account for the existence of molecules we must account for the predominance of the attractive interactions. We shall give general arguments to show that this is so, first in terms of the energy of a molecule, relative to the energies of the constituent atoms, and secondly, in terms of the forces acting on the nuclei in a molecule.

   In order to determine what attractive and repulsive interactions are possible in a molecule, consider an instantaneous configuration of the nuclei and electrons in a hydrogen molecule (Fig. 6-1). When the two atoms are initially far apart (the distance R is very large) the only potential interactions are the attraction of nucleus A for electron number (1) and the attraction of nucleus B for electron number (2). When R is comparable to the diameter of an atom (A and B are close enough to form a molecule) then new interactions appear. Nucleus A will now attract electron (2) as well as (1) and similarly nucleus B will attract electron (1) as well as (2). These interactions are indicated by the four solid lines in Fig. 6-1 connecting pairs of particles which attract one another.

Fig. 6-1.  One possible set of the instantaneous relative positions of the electrons and nuclei in an H., molecule. The dashed lines represent the repulsive interactions between like charges and the solid lines indicate the attractive interactions between opposite charges.

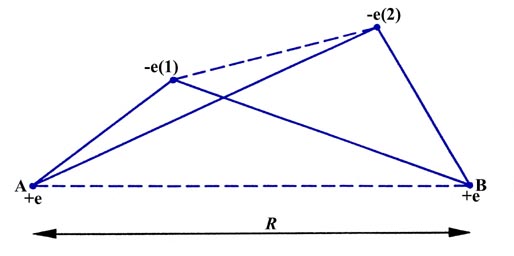
      The number of attractive interactions has been doubled from what it was when the atoms were far apart. However, the reduction in R introduces two repulsive interactions as well, indicated by the dashed lines joining charges of like sign in Fig. 6-1. The two electrons now repel one another as do the two nuclei. If the two atoms are to remain together to form a molecule, the attractive interactions must exceed the repulsive ones. It is clear from Fig. 6-1 that the new attractive interactions, nucleus A attracting electron (2) and nucleus B attracting electron (1), will be large only if there is a high probability of both electrons being found in the region between the nuclei. When in this region, both electrons are strongly attracted by both nuclei, rather than by just one nucleus as is the case when the atoms are far apart.

    When the average potential energy is calculated by quantum mechanics, the attractive interactions are found to predominate over the repulsive ones because quantum mechanics does indeed predict a high probability for each electron being in the region between the nuclei. This general consideration of the energy demonstrates that electron density must be concentrated between the nuclei if a stable molecule is to be formed, for only in this way can the attractive interaction be maximized. We can be much more specific in our analysis of this problem if we discuss a molecule from the point of view of the forces acting on the nuclei. However, we must first state some general conclusions of quantum mechanics regarding molecular systems.

   In the atomic case we could fix the position of the nucleus in space and consider only the motion of the electrons relative to the nucleus. In molecules, the nuclei may also change positions relative to one another. This complication can, however, be removed. The nuclei are very massive compared to the electrons and their average velocities are consequently much smaller than those possessed by the electrons. In a classical picture of the molecule we would see a slow, lumbering motion of the nuclei accompanied by a very rapid motion of the electrons. The physical implication of this large disparity in the two sets of velocities is that the electrons can immediately adjust to any change in the position of the nuclei. The positions of  the nuclei determine the potential field in which the electrons move. However, as the nuclei change their positions and hence the potential field, the electrons can immediately adjust to the new positions. Thus the motion of  the electrons is determined by where the nuclei are but not by how fast the nuclei are moving. We may, because of this fact, discuss the motions of the electrons and of the nuclei separately.

   For a given distance between the nuclei we obtain the energy, the wave function and the electron density distribution of the electrons, the nuclei being held in fixed positions. Then the distance between the nuclei is changed to a new value, and the calculation of the energy, wave function and electron density distribution of the electrons is performed again. This process, repeated for every possible internuclear distance, allows us to determine how the energy of the electrons changes as the distance between the nuclei is changed. More important for our present discussion, we may concern ourselves only with the motion of the electrons and hold the nuclei stationary at some particular value for the internuclear distance R.

   The energy of the electrons in a molecule is quantized, as it is in atoms. When the nuclei are held stationary at some fixed value of R, there are a number of allowed energy levels for the electrons. There are, however, no simple expressions for the energy levels of a molecule in terms of a set of quantum numbers such as we found for the hydrogen atom. In any event we shall be concerned here only with the first or lowest of the energy levels for a molecule. As in the case of atoms, there is a wave function which governs the motion of all the electrons for each of the allowed energy levels. Each wave function again determines the manner in which the electronic charge is distributed in three-dimensional space.

   The electron density distribution for a molecule is best illustrated by means of a contour map, of the kind introduced earlier in the discussion of the hydrogen atom. Figure 6-2 shows a contour map of the charge distribution for the lowest, or most stable state of the hydrogen molecule. Imagine a hydrogen molecule to be cut in half by a plane which contains the nuclei.The amount of electronic charge at every point in space is determined, and all points having the same value for the electron density in the plane are joined by a line, a contour line. Also shown is a profile of the contour map along the internuclear axis. A profile illustrates the variation in the charge density along a single axis.

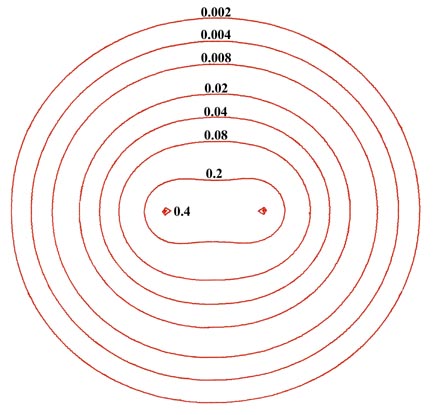
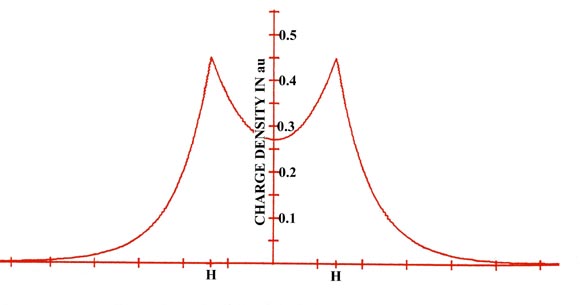
Fig. 6-2.  A contour map of the electron density distribution (or the molecular charge distribution) for H₂ in a plane containing the nuclei. Also shown is a profile of the density distribution along the internuclear axis. The internuclear separation is 1.4 au. The values of the contours increase in magnitude from the outermost one inwards towards the nuclei. The values of the contours in this and all succeeding diagrams are given in au; 1 au = e/a_o³ = 6.749 e/ų.

   The electron density contours of highest value are in the region of each nucleus. Thus the negative charge is concentrated in the region of the nuclei in a molecule as well as in an atom. The next highest concentration of negative charge is found in the region between the nuclei. It is the negative charge in this region which is strongly attracted by both nuclei and which results in the attractive interactions exceeding the repulsive ones in the formation of the molecule from the atoms. Most of the density contours envelope both nuclei. The density distributions of the two atoms have been merged together in the formation of the molecule.

   The same contour map would be obtained for any plane through the nuclei. Therefore, in three-dimensional space the hydrogen molecule would appear to be an ellipsoidal distribution of negative charge. Most of the electronic charge is concentrated along the internuclear axis and becomes progressively more diffuse at large distances from the centre of the molecule. Recall that the addition of all the charge in every small volume element of space equals the total number of electrons which in the case of the hydrogen molecule is two. The volume of space enclosed by the outer contour in Fig. 6-2 contains over 99% of the total electronic charge of the hydrogen molecule.