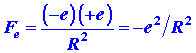An Introduction to the Electronic Structure of Atoms and Molecules

In the light of the above discussion of a molecular electron density distribution, we may regard a molecule as two or more nuclei imbedded in a rigid three-dimensional distribution of negative charge. There is a theorem of quantum mechanics which allows us to make direct use of this picture of a molecule. This theorem states that the force acting on a nucleus in a molecule may be determined by the methods of classical electrostatics. The nuclei in a molecule repel one another, since they are of like charge. This force of repulsion, if unbalanced, would push the nuclei apart and the molecule would separate into atoms. In a stable molecule, however, the nuclear force of repulsion is balanced by an attractive force exerted by the negatively-charged electron density distribution. The usefulness of this approach lies in the fact that we may account for and discuss the stability of molecules in terms of the classical concept of a balance between the electrostatic forces of attraction and repulsion. We can illustrate this method and arrive at some results of a general nature by considering in detail the forces acting on the nuclei in the hydrogen molecule.

   The charge on a hydrogen nucleus is +e and the force of repulsion acting on either nucleus is
 

where R is the internuclear distance. This force obviously acts to push the two nuclei apart (Fig. 6-3).

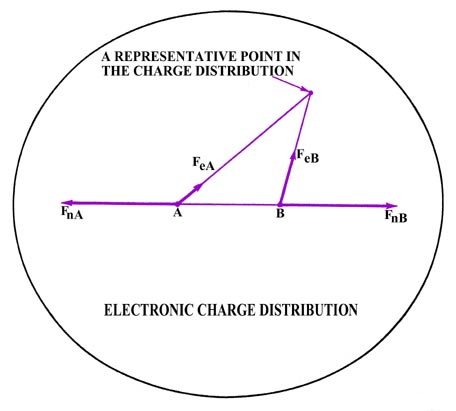
Fig. 6-3.  The forces acting on the nuclei in H₂. Only one outer contour of the electron density distribution is shown. Over 99% of the total electronic charge is contained within this contour.

   The attractive force which balances this force of repulsion and draws the nuclei together is exerted by the negatively-charged electron density distribution. The density distribution is treated as a rigid distribution of negative charge in space. Each small element of this charge distribution exerts a force on the nuclei, illustrated in Fig. 6-3 for one such small charge point. The forces it exerts on the nuclei are labelled F_eA and F_eB. The total amount of negative charge in the electron density distribution must correspond to some integral number of electrons. However, the amount of negative charge in each small region of space will in general correspond to some fraction of one electronic charge.

  The electronic force of attraction F_eA or F_eB may be equated to two components, one along the bond, and one perpendicular to it. The density distribution is symmetric with respect to the internuclear axis, i.e., for every charge point above the axis there must, by symmetry, be another point of equal charge at the corresponding place beneath the internuclear axis. The symmetrically related charge point will exert the same force along the bond, but the component perpendicular to the bond will be in the opposite direction. Thus the perpendicular forces of attraction exerted on the nuclei are zero (Fig. 6-4) and we may confine our attention to the components of the attractive force along the bond.

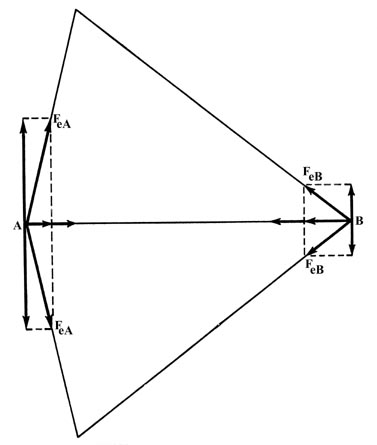
Fig. 6-4.  The two components of force along the bond add together while the two perpendicular components cancel at both A and B.

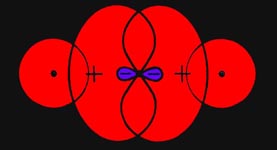
   It is obvious that all of the charge elements which are in the general region between the two nuclei will exert forces which draw the two nuclei together. The force exerted by the density in this region acts in opposition to the force of nuclear repulsion and binds the two nuclei together. It is also clear that a charge element in the region behind either nucleus will exert a force which tends to increase the distance between the nuclei (Fig. 6-5).

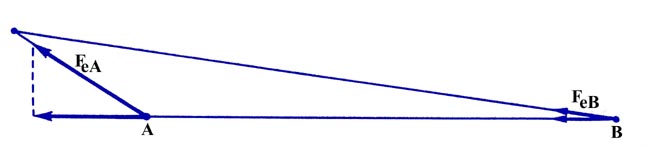
Fig. 6-5.  The component of F_eA along the bond is greater than the corresponding component of F_eB.

Since the charge element is closer to nucleus A than it is to nucleus B, the component of the force on A along the bond will be greater than the component of the force on B along the bond. Thus the effect of density in this region will be to separate the molecule into atoms.

   There must also be a line on which the density exerts the same force on both nuclei and thus neither increases nor decreases R because the charge density in one region draws the nuclei together and in another draws them apart. The charge element shown in Fig. 6-6 exerts the same force along the bond on both A and B even though it is closer to B than it is to A. 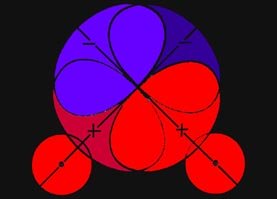Although the total force F_eB is much larger than F_eA, F_eB is directed almost perpendicular to the bond axis and thus its component along the bond is quite small and equal to the component of F_eA along the bond. Charge density on either of the two curves shown in Fig. 6-6 exerts equal forces on both of the nuclei along the bond, and such charge density will not tend to increase or decrease the distance between the nuclei. Thus these two curves  (surfaces in three dimensions) divide the space in a molecule into a binding region and an antibinding region. Any charge density between the two boundary curves, in the binding region, draws the two nuclei together while any charge density in the hatched region behind either curve, the antibinding region, exerts unequal forces on the nuclei and separates the molecule into atoms.

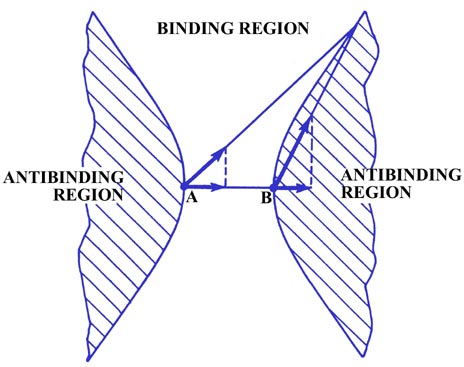
Fig. 6-6. The boundary curves which separate the binding from the antibinding regions in a homonuclear diatomic molecule.

   A chemical bond is thus the result of the accumulation of negative charge density in the region between the nuclei to an extent sufficient to balance the nuclear forces of repulsion. This corresponds to a state of electrostatic equilibrium as the net force acting on each nucleus is zero for this one particular value of the internuclear distance. If the distance between the nuclei is increased from the equilibrium value, the nuclear force of repulsion is decreased. At the same time the force of attraction exerted by the electron density distribution is increased as the binding region is increased in size. Thus when R is increased from its equilibrium value there are net forces of attraction acting on the nuclei which pull the two nuclei together again. A definite force would have to be applied to overcome the force of attraction exerted by the electron density distribution and separate the molecule into atoms. Similarly, if the value of R is decreased from its equilibrium value,   the force of nuclear repulsion is increased over its equilibrium value. At the same time, the attractive force exerted by the electron density is decreased, because the binding region is decreased in size. In this case there will be a net force of repulsion pushing the two nuclei apart and back to their equilibrium separation. There is thus one value of R for which the forces on the nuclei are zero and the whole molecule is in a state of electrostatic equilibrium.

     The division of the space around a molecule into a binding and an antibinding region shows where charge density must be concentrated in order to obtain a stable chemical bond. The next question which must be answered is,  "How  much  charge  must  be  placed  in  the  binding  region  to  achieve electrostatic equilibrium?" For example, we might consider the possibility of forming a molecule by bringing together two atoms, each with its own atomic distribution of charge, and simply allow the two atomic charge distributions to overlap without deforming in any way. This would result in the accumulation of approximately twice as much charge density in the binding region as in either of the antibinding regions behind the nuclei. Would this doubling of the charge density in the region between the nuclei be sufficient to balance the nuclear forces of repulsion? Let us answer this question for the simple case of two hydrogen atoms forming molecular hydrogen, but again the result will be general.

    The most stable state of the hydrogen molecule is obtained when two hydrogen atoms, each in its most stable atomic state, approach one another. The ground state of a hydrogen atom is obtained when the electron is in the 1s orbital. The density distribution around each hydrogren nucleus is the spherical one which we discussed previously in some detail. We shall first calculate the force on one of the hydrogen nuclei resulting when the two atoms are very far apart. The situation is represented in Fig. 6-7 where each atomic charge distribution is represented by a single outer circular contour. This contour is to define a sphere which in three-dimensions contains essentially all of the electronic charge of each atom.

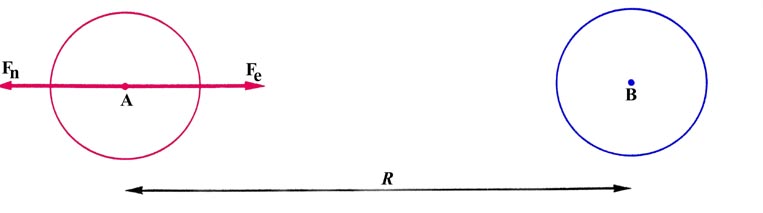
Fig. 6-7. The forces acting on nucleus A at a large internucleus distances, R.

   Consider the forces exerted on nucleus A. The force of nuclear repulsion is just
 

The atomic charge density centred on nucleus A exerts no net force on this nucleus as it pulls equally in every direction because of its spherical symmetry. There is, however, a net force of attraction due to the single electronic charge dispersed in the atomic distribution of B. A theorem of classical electrostatics states that the force exerted by a spherical charge distribution on a point charge lying outside of the charge distribution is equal to the  force which would be obtained if all the charge in the distribution were concentrated at its centre. Nucleus A is a point charge which lies outside of the spherical charge distribution centred on B. Thus the force exerted on  nucleus A by this charge distribution is just
 

as the total amount of charge contained in the distribution is that of one electron. The total force acting on nucleus A is
 

 A zero force is the expected answer when the two atoms are very far apart.

    Can we again balance the forces for a value of R which is of the order of magnitude of an atomic diameter, i.e., typical of the values of R found in molecules? At this value of R, each nucleus will have penetrated the charge density surrounding the other nucleus. Recall that in this calculation we insist upon the atomic charge densities remaining spherical and our molecular charge density is obtained by allowing the two rigid atomic charge distributions to overlap one another (Fig. 6-8).

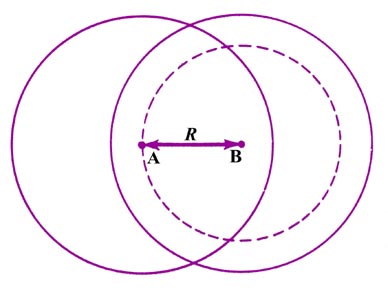Fig. 6-8. The forces exterted on the nucleus A for the overlap of rigid atomic charge distributions. Only the charge density on B which is contained in the sphere of radius R exerted a force on nucleus A.

The force of nuclear repulsion in this case is still given by
 

where the value of R is much less than in the previous calculation. Since the charge distribution on A is still spherical in shape, it exerts no net force on nucleus A. The force exerted on nucleus A by the charge density on B can again be calculated by the theorem referred to previously. However, nucleus A no longer lies outside of all the charge density on B. The value of R is significantly less than the radius of the charge distribution on B. All the charge density on B which lies within the sphere defined by the bond length R again exerts a force on nucleus A, equal to that obtained if all this density were situated at the B nucleus. The theorem referred to previously shows that the density on B which lies outside of this sphere defined by R exerts no net force on nucleus A.

   Since R is less than the diameter of the charge distribution, the amount of negative charge contained in a sphere of radius R will be less than that of one electron. The observed value of R for the hydrogen molecule is 1.4 au and reference to the data given previously for the 1s orbital density for the hydrogen atom shows that a sphere of radius 1.4 would contain approximately one half of an electronic charge. The electrostatic force of attraction exerted on nucleus A is, therefore,
 

The net force on nucleus A is
 

There is a net force of repulsion exerted on nucleus A under these conditions. If R were decreased still further, nucleus A would penetrate the charge density around B to an even greater extent and "see" even more of the nuclear charge on B. The force on the nuclei will thus be repulsive for all finite values of R.

   This is an important result as it shows that the density distribution in a molecule cannot be considered as the simple sum of the two atomic charge densities. The overlap of rigid atomic densities does not place sufficient charge density in the binding region to overcome the nuclear force of  repulsion. We conclude that the original atomic charge distributions must be distorted in the formation of a molecule, and the distortion is such that charge density is concentrated in the binding region between the nuclei. A quantum mechanical calculation predicts this very result. The calculation shows that there is a continuous distortion of the original atomic density distributions, a distortion which increases as the internuclear distance decreases. This is illustrated in Fig. 6-9 for the approach of two hydrogen atoms to form the hydrogen molecule.

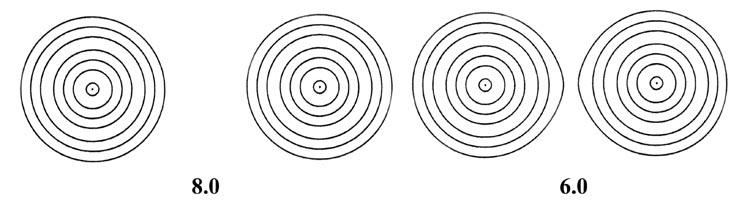
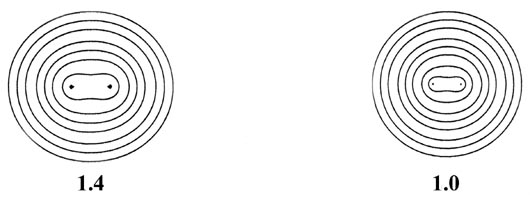
Fig. 6-9.  A series of electron density contour maps illustrating the changes in the electron charge distribution during the approach of two H atoms to form H₂. The internuclear distance R in units of au is indicated beneath each map. At R = 8 the atomic densities appear to be undistorted. At R = 6 the densities are distorted but still essentially separate. As R is further decreased, charge density contours of increasing value envelope both nuclei, and charge density is accumulated at the positions of the nuclei and in the internuclear region. The values of the contours in au increase from the outermost to the innermost one in the order 2 ´ 10^-n, 4 ´ 10^-n, 8 ´ 10^-n, for decreasing values of n beginning with n = 3. Thus the outermost contour in each case is 0.002 au and the value of the innermost contour for R = 1.0 au, for example, is 0.4.

    The changes in the original atomic density distributions caused by the formation of the chemical bond may be isolated and studied directly by  the construction of a density difference distribution. Such a distribution is obtained by subtracting the density obtained from the overlap of the undistorted atomic densities separated by a distance R, from the molecular charge distribution evaluated at the same value of R. Wherever this density difference is positive in value it means that the electron density in the molecule is greater than that obtained from the simple overlap of the original atomic densities. Where the density difference is negative, it means that there is less density at this point in space in the molecule than in the distribution obtained from the overlap of the original atomic distributions. Such a density difference map thus provides a detailed picture of the net reorganization of the charge density of the separated atoms accompanying the formation of a molecule.

   We have just proven that the density distribution resulting from the overlap of the undistorted atomic densities does not place sufficient charge density in the binding region to balance the forces of nuclear repulsion. The regions of charge increase in the density difference maps are, therefore, the regions to which charge is transferred relative to the separated atoms to obtain a state of electrostatic equilibrium and hence a chemical bond. From this point of view a density difference map provides us with a picture of the "bond density."

   Figure 6-10 shows a set of density difference or bond density maps for the approach of two hydrogen atoms to form the hydrogen molecule. At very large separations, for example at 8 au, the density distribution on each atom is polarized in the direction of the approaching atom. Charge density has been transferred from the antibinding region behind each nucleus to the binding region immediately in front of each nucleus. Thus even at large separations the atomic density distributions are no longer spherical. We noted in our discussion of the approach of two rigid hydrogen atoms that a spherical charge distribution does not exert a net force on the nucleus on which it is centred. Each polarized atomic charge distribution does, however, exert an attractive force on its nucleus. The polarized densities place more charge on the binding side of each nucleus than on the antibinding side. These long-range attractive forces, called van der Waals' or dispersion forces, could be aptly described as a "bootstrap effect" as each nucleus is pulled by its own charge density. All pairs of neutral molecules undergo this type of polarization as a result of the long-range interactions between them, and there are attractive forces operative between all pairs of molecules out to very large distances. Although the long-range polarizations and the resulting forces of attraction are very weak, they are of extreme importance. They are commonly referred to as van der Waals forces and are solely responsible for the binding observed in certain kinds of solids, solid helium for example. This will be discussed more fully later.

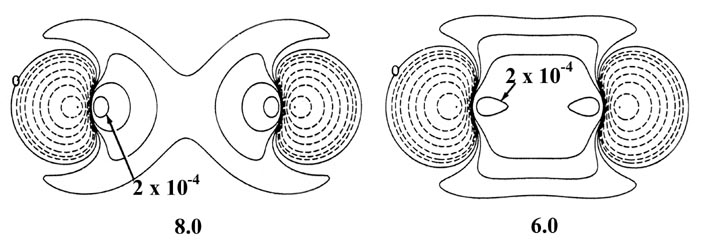
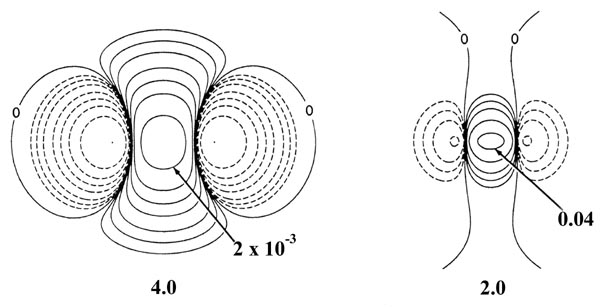
Fig. 6-10.  Density difference distribution (molecular minus atomic) for the approach of two H atoms. These maps indicate the changes in the atomic densities caused by the formation of a molecule. The solid contours represent an increase in charge density over the atomic case, while the dashed contours denote a decrease in the charge density relative to the atomic densities. Since the changes in the charge density are much smaller for large values of R than for small values of R two different scales are used. The solid and dashed contours increase (+) or decrease (-) respectively from the zero contour in the order ±2 ´ 10^-n, ±4 ´ 10^-n, ±8 ´ 10^-n au for decreasing values of n. The maps for R = 8.0, 6.0 and 4.0 au begin with n = 5 and those for R = 2.0, 1.4 and 1.0 au begin with n = 3. The zero contour and the value of the innermost positive contour are indicated in each case. Note the continuous increase in charge density in the region between the nuclei as R is decreased.

     At 6.0 au the density increase in the binding region is common to both nuclei, and for distances less than 6.0 au the system can no longer be described as two polarized hydrogen atoms. The distortions of the original densities caused by the transfer of charge to the binding region is so great that the individual character of the atomic densities is no longer discernible. The magnitude of the attractive force (which is negative in sign) exerted on the nuclei by this accumulation of charge density in the binding region increases rapidly for distances less than 4.5 au (Fig. 6-11).

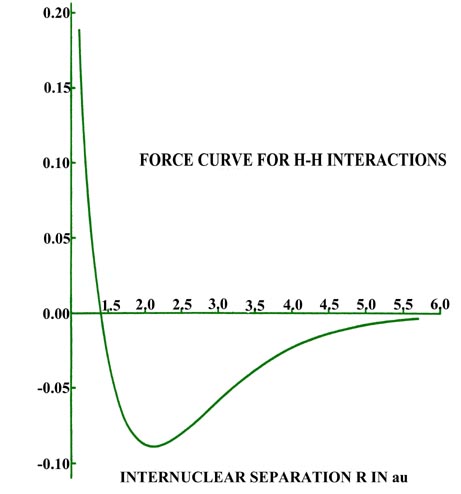Fig. 6-11. The force on an H nucleus in H2 as a function of the internuclear separation. An attractive force is negative in sign; a replusive one, positive.

The attractive force reaches a maximum at 2.1 au. The density difference diagrams indicate that for distances as small as 2.0 au, the density increase is confined to the region between the nuclei. For separations smaller than  2.0 au an increasing amount of charge density is transferred to the anti-binding regions behind each nucleus. Because of this, the attractive force on the nuclei decreases rapidly with a further decrease in R until at R = 1.4 au, the net attractive force exerted by the charge density just balances the force of nuclear repulsion (Fig. 6-11). A state of electrostatic equilibrium is reached, and a chemical bond is formed. A further decrease in R leads to a force of repulsion. More charge density is transferred to the antibinding regions, and the force exerted by this charge density, acting in concert with the increase in the force of nuclear repulsion, outweighs the attractive force exerted by the charge density in the binding region.

   The same changes in density are depicted in Fig. 6-12, which is a series of profiles along the internuclear axis of the density difference maps shown in Fig. 6-10. The profile maps illustrate in a striking fashion the build-up of charge density in the region between the nuclei.

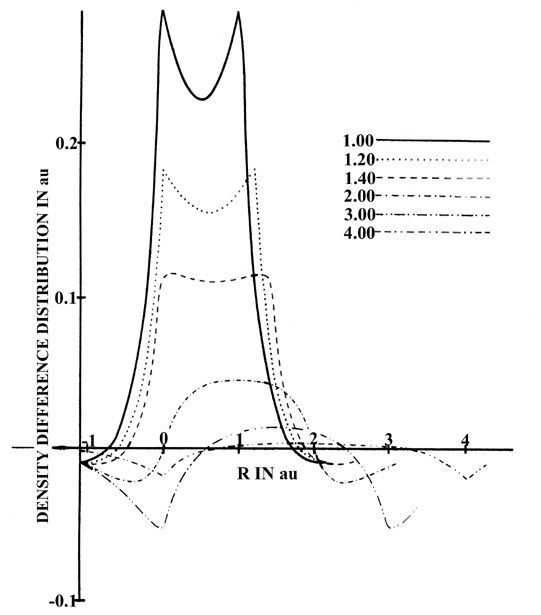Fig. 6-12.  Profiles of the density difference along the internuclear axis for H2at a series of internuclear separations. One nucleus is held fixed, and the other is moved relative to it. The separations are indicated on the diagram.

   The formation of any chemical bond is qualitatively similar to the changes in the charge distribution and in the forces exerted on the nuclei as found for the hydrogen molecule. We must now inquire into the conditions which determine whether or not sufficient charge density can be accumulated in the binding region to yield a stable molecule. Since not all atoms form chemical bonds, clearly such conditions must exist.