An Introduction to the Electronic Structure of Atoms
and Molecules
Dr. Richard F.W. Bader
Professor of Chemistry / McMaster University / Hamilton,
Ontario
|
Classification of Chemical Bonds
To make a quantitative assessment of the type of binding present in
a particular molecule it is necessary to have a measue of the extent of
charge transfer present in the molecule relative to the charge distributions
of the separated atoms. This information is contained in the density difference
or bond density distribution, the distribution obtained by subtracting
the atomic densities from the molecular charge distribution. Such a distribution
provides a detailed measure of the net reorganization of the charge densities
of the separated atoms accompanying the formation of the molecule.
The density distribution resulting from the overlap of
the undistorted atomic densities (the distribution which is subtracted
from the molecular distribution) does not place sufficient charge density
in the binding region to balance the nuclear forces of repulsion.
The regions of charge increase in a bond density map are, therefore, the
regions to which charge is transferred relative to the separated atoms
to obtain a state of electrostatic equilibrium and hence a chemical bond.
Thus we may use the location of this charge increase relative to the positions
of the nuclei to characterize the bond and to obtain an explanation for
its electrostatic stability.
In covalent binding we shall find that the forces binding
the nuclei are exerted by an increase in the charge density which is shared
mutually between them. In ionic binding both nuclei are bound by a charge
increase which is localized in the region of a single nucleus.
Covalent Binding
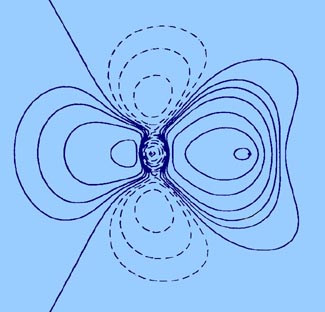
The bond density map of the nitrogen molecule (Fig.
7-2) is illustrative of the characteristics of covalent binding.
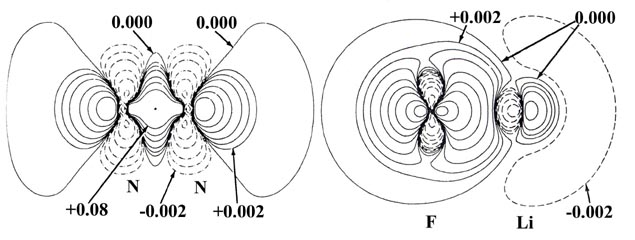
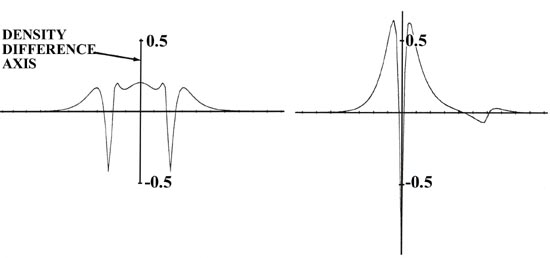
Fig. 7-2. Bond density (or density difference)
maps and their profiles along the internuclear axis for N2 and
LiF. The solid and dashed lines represent an increase and a decrease respectively
in the molecular charge density relative to the overlapped atomic distributions.
These maps contrast the two possible extremes of the manner in which the
original atomic charge densities may be redistributed to obtain a chemical
bond. Click here
for contour values.
The principal feature of this map is a large accumulation of charge
density in the binding region, corresponding in this case to a total increase
of one quarter of an electronic charge. As noted in the study of the total
charge distribution, charge density is also
transferred to the antibinding regions of the nuclei but the amount
transferred to either region, 0.13 e-, is less than is
accumulated in the binding region. The charge density of the original atoms
is decreased in regions perpendicular to the bond at the positions of the
nuclei. In three dimensions, the regions of charge deficit correspond to
two continuous rings or roughly doughnut-shaped regions encircling the
bond axis.
The increase in charge density in the antibinding regions
and the removal of charge density from the immediate regions of the nuclei
result in an increase in the forces of repulsion exerted on the nuclei,
forces resulting from the close approach of the two atoms and from the
partial overlap of their density distributions. The repulsive forces are
obviously balanced by the forces exerted on the nuclei by the shared
increase in charge density located in the binding region.
A bond is classified as covalent when the bond density
distribution indicates that the charge increase responsible for the binding
of the nuclei is shared by both nuclei. It is not necessary for covalent
binding that the density increase in the binding region be shared equally
as in the completely symmetrical case of N2.
We shall encounter heteronuclear molecules (molecules with different nuclei)
in which the net force binding the nuclei is exerted by a density increase
which, while shared, is not shared equally between the two nuclei.
The pattern of charge rearrangement in the bond density
map for N2 is, aside from the accumulation
of charge density in the binding region, quite distinct from that found
for H2 (Fig.
6-10), another but simpler example of covalent binding. The pattern
observed for nitrogen, a charge increase concentrated along the bond axis
in both the binding and antibinding regions and a removal of charge density
from a region perpendicular to the axis, is characteristic of atoms which
in the orbital model of bonding employ p atomic orbitals in forming
the bond. Since a p orbital concentrates charge density on opposite
sides of a nucleus, the large buildup of charge density in the antibinding
regions is to be expected.
In the orbital theory of the hydrogen molecule, the
bond is the result of the overlap of s orbitals. The bond density
map in this case is characterized by a simple transfer of charge from the
antibinding to the binding region since s orbitals do not possess
the strong directional or nodal properties of p orbitals. Further
examples of both types of charge rearrangements or polarizations will be
illustrated below.
Ionic Binding
We shall preface our discussion of the bond density map for ionic binding
with a calculation of the change in energy associated with the formation
of the bond in LiF. While the calculation will be relatively crude and
based on a very simple model, it will illustrate that the complete transfer
of valence charge density from one atom to another in forming a molecule
is in certain cases energetically possible.
Lithium possesses the electronic configuration
1s22s1
and is from group IA of the periodic table. It possesses a very low ionization
potential and an electron affinity which is zero for all practical purposes.
Fluorine is from group VIIA and has a configuration 1s22s22p5.
It possesses a high ionization potential and a high electron affinity.
The following calculation will illustrate that the 2s electron of
Li could conceivably be transferred completely to the 2p shell of
orbitals on F in which there is a single vacancy. This would result in
the formation of a molecule best described as Li+F-,
and in the electron configurations 1s2 for
Li+ and 1s22s22p6
for F-.
We can calculate the energy change for the reaction
in stages. The energy which must be supplied to ionize the 1s electron
on the Li atom is:
| (1) |
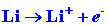
|
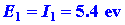
|
The energy released when an electron combines with an F atom is given by
the electron affinity of F:
| (2) |
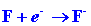
|
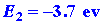
|
The two ions are oppositely charged and will attract one another. The energy
released when the two ions approach one another from infinity to form the
LiF molecule is easily estimated. To a first approximation it is simply
-e2/R where R is the
final equilibrium distance between the two ions in the molecule:
| (3) |
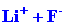
|
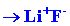 |
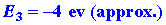
|
|
(large distance apart)
|
(at R) |
|
The sum of these three reactions gives
and the overall change in energy is the sum of the three energy changes,
or approximately -2 ev. The species Li+F- possesses
a lower energy than the separated Li and F atoms and should therefore be
a stable molecule.
The transfer of charge density from lithium to fluorine
is very evident in the bond density map for LiF (Fig.
7-2). The charge density of the 2s electron on the lithium atom
is a very diffuse distribution and consequently the negative contours in
the bond density map denoting its removal are of large spatial extent but
small in magnitude. The principal charge increase is nearly symmetrically
arranged about the fluorine nucleus and is completely encompassed by a
single nodal surface. The total charge increase on fluorine amounts to
approximately one electronic charge. The charge increase in the antibinding
region of the lithium nucleus corresponds to only 0.01 electronic charges.
(The great disparity in the magnitudes of the charge increases on lithium
and fluorine are most strikingly portrayed in the profile of the bond density
map, also shown in Fig. 7-2) It is equally important
to realize that the charge increase on lithium occurs within the region
of the 1s inner shell or core density and not in the region of the
valence density. Thus the slight charge increase on lithium is primarily
a result of a polarization of its core density and not of an accumulation
of valence density.
The pattern of charge increase and charge removal in the
region of the fluorine, while similar to that for a nitrogen nucleus in
N2, is much more symmetrical, and the charge
density corresponds very closely to the distribution obtained from a single
2ps electron. Thus the simple orbital
model of the bond in LiF which describes the bond as a transfer of the
2s electron on lithium to the single 2ps
vacancy on fluorine is a remarkably good one.
While the bond density map for LiF substantiates the concept
of charge transfer and the formation of Li+ and F-
ions it also indicates that the charge distributions of both ions are polarized.
The charge increase in the binding region of fluorine exceeds slightly
that in its antibinding region (the F- ion is polarized towards
the Li+ ion) and the charge distribution of the Li+
ion is polarized away from the fluorine. A consideration of the forces
exerted on the nuclei in this case will demonstrate that these polarizations
are a necessary requirement for the attainment of electrostatic equilibrium
in the face of a complete charge transfer from lithium to fluorine.
Consider first the forces acting on the nuclei in
the simple model of the ionic bond, the model which ignores the polarizations
of the ions and pictures the molecule as two closed-shell spherical ions
in mutual contact. If the charge density of the Li+ ion
is spherical it will exert no net force on the lithium nucleus. The F-
ion possesses ten electrons and, since the charge density on the F-
ion is also considered to be spherical, the attractive force this density
exerts on the Li nucleus is the same as that obtained for all ten electrons
concentrated at the fluorine nucleus. Nine of these electrons will screen
the nine positive nuclear charges on fluorine from the lithium nucleus.
The net force on the lithium nucleus is, therefore, one of attraction because
of the one excess negative charge on F.
For the molecule to be stable, the final force on the lithium
nucleus must be zero. This can be achieved by a distortion of the spherical
charge distribution of the Li+ ion. If a small amount of the
1s charge density on lithium is removed from the region adjacent
to fluorine and placed on the side of the lithium nucleus away from the
fluorine, i.e., the charge distribution is polarized away from the fluorine,
it will exert a force on the lithium nucleus in a direction away from the
fluorine. Thus the force on the lithium nucleus in an ionic bond can be
zero only if the charge density of the Li+ ion is polarized
away from the negative end of the molecule.
A similar consideration of the forces exerted on the fluorine
nucleus demonstrates that the F- ion density must also be polarized.
The fluorine nucleus experiences a net force of repulsion because of the
presence of the lithium ion. The two negative charges centred on lithium
screen only two of its three nuclear charges. Therefore, the charge density
of the F- ion must be polarized towards the lithium
in order to exert an attractive force on the fluorine nucleus which will
balance the repulsive force arising from the presence of the Li+
ion. Thus both nuclei in the LiF molecule are bound by the increase in
charge density localized in the region of the fluorine.
The charge distribution of a molecule with an ionic bond
will necessarily be characterized not only by the transfer of electronic
charge from one atom to another, but also by a polarization of each of
the resulting ions in a direction counter to the transfer of charge, as
indicated in the bond density map for LiF.
The bond density maps for N2
and LiF are shown side by side to provide a contrast of the changes in
the atomic charge densities responsible for the two extremes of chemical
binding. In a covalent bond the increase in charge density which
binds both nuclei is shared between them. In an ionic bond both nuclei
are bound by the forces exerted by the charge density localized on a single
nucleus. It must be stressed that there is no fundamental difference
between the forces responsible for a covalent or an ionic bond. They are
electrostatic in each case.