An Introduction to the Electronic Structure of Atoms and Molecules

Contour maps of the charge distributions for the stable homonuclear diatomic molecules formed from the second-row atoms (Fig. 7-3) provide further examples of covalent binding. The maps illustrate the relative tightness of binding of the density distributions, the density in Li₂ for example being much more diffuse than that in N₂. Two important physical dimensions for a molecule are the bond length and the molecular size. The bond length of a molecule may be directly determined (by X-ray diffraction techniques or by spectroscopic methods) but the size of a molecule cannot be as precisely defined or measured. However, molecular diameters may be inferred from measurements of the viscosity of gas phase molecules and from X-ray crystallographic studies on the structures of molecular crystals such as solid N₂ and O₂.

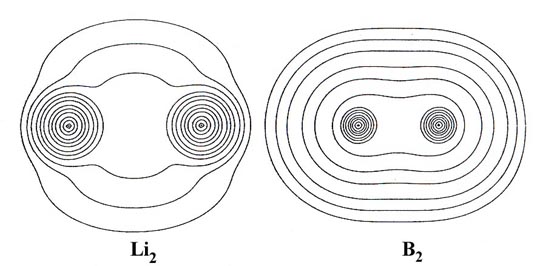
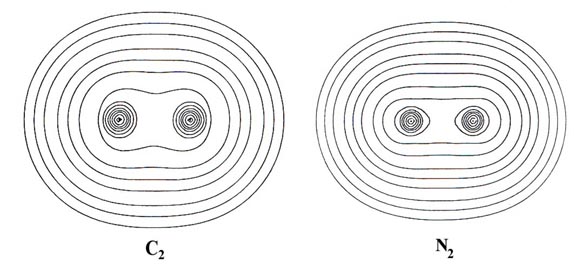
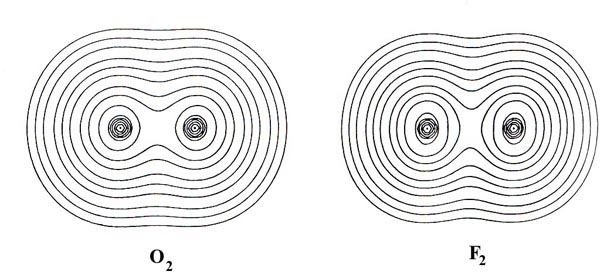
Fig. 7-3. Countour maps of the molecular charge distribution for the stable homonuclear diatomic molecules Li₂to F₂. Click here for countour values.

    In general over 95% of the molecular charge lies within the 0.002 contour  (the outermost contour illustrated in the density maps) and it has been found that the dimensions of this contour agree well with the experimental estimates of molecular sizes. The length and width of each molecule, defined respectively as the distance between the intercepts of the 0.002 contour on the molecular axis and on a line perpendicular to the axis and passing through its mid-point, are given in Table 7-1 along with the experimental bond lengths R_e

   There is only a rough correlation between the bond length and the overall length of the molecule. Thus the lengths of N₂ and O₂ are in the reverse order of their bond lengths, as is also roughly true experimentally. The lithium molecule has the largest bond length but a molecular length only slightly larger than that of C₂. There are two factors which must be considered in understanding the length of a molecule, the bond length and the rate at which the density falls off from the nucleus on the side away from the bond. Table 7-1 lists the distance from the nucleus to the 0.002 contour in the molecule, i.e., the radius of the nonbonded charge density, and the radius of the same contour in the isolated atom. With the exception of Li₂, this distance in the molecule is almost identical to the value in the isolated atom. Thus the contribution of the two end lengths, beyond the nuclear separation, to the overall length of a molecule is largely determined by how tightly the density is bound in the unperturbed atom. The binding of the atomic densities increases from Li across to F, so that Li and Be are large and diffuse and N, 0, and F progressively tighter and more compact. Therefore F₂ is smaller in size than N₂ or C₂ even though it possesses a greater bond length because the density in the F atom is more tightly bound than that in the C or N atoms. The Li molecule differs from the others in that its length is considerably less than expected considering the diffuse nature of its atomic density. In this case the molecular length is not approximately equal to the sum of R_e and twice the "atomic" radius. This is, however, easily understood since in the Li atom only one valence-shell electron is present and in the molecule the charge density of this electron is concentrated almost exclusively in the binding region. This is further illustrated by using instead of the 0.002 contour of Li the 0.002 contour of the 1s² shell of Li⁺, which is in fact equal to the value listed in Table 7-1 for the Li₂ molecule.

   An estimate of the size of a peripheral atom in a molecule can thus be obtained by taking the sum of ½R_e from a suitable source and the atomic radius as defined by the 0.002 contour of the atom (except for Li, Na, etc., where the core radius should be used).

   The bond density maps for the second-row homonuclear diatomic molecules (Fig. 7-4) indicate that the original atomic densities are distorted so as to place charge in the antibinding as well as in the binding regions.

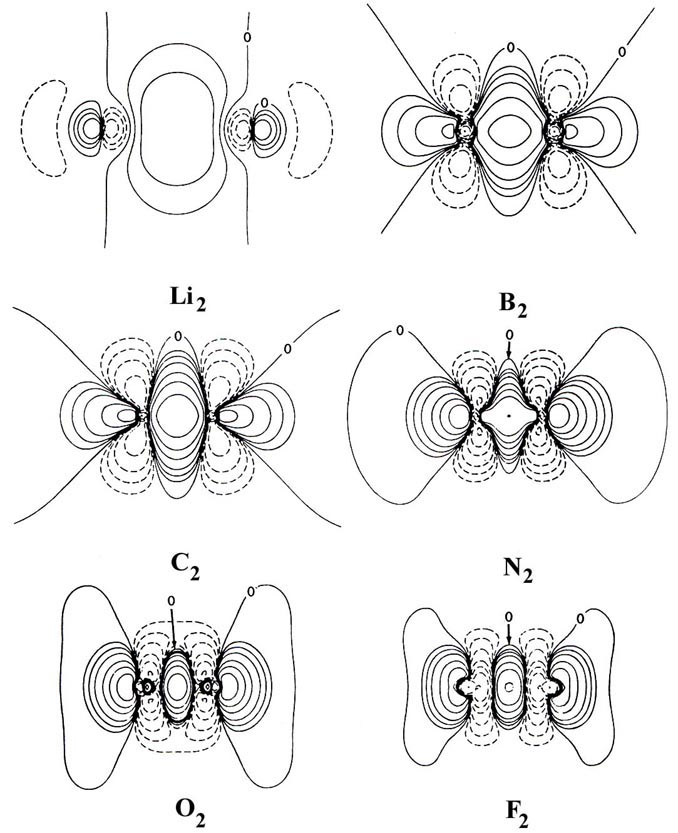
Fig. 7-4. Bond density maps for the homonuclear diatomic molecules. Click here for contour values

Apart from Li₂ the pattern of charge increase and charge removal in these molecules is similar to that discussed previously for N₂, a pattern ascribed to the participation of 2ps orbitals in the formation of the bond. Only Li₂ approximates the simple picture found for H₂ of removal of charge from the antibinding region and a buildup in the binding region. For the remaining molecules charge density is increasingly accumulated along the bond axis in both the binding and antibinding regions.

   The total accumulation of electronic charge represented by the regions of positive contours in the binding and antibinding regions of the bond density maps are listed in Table 7-2.

These figures show that in O₂ and F₂ a greater amount of charge is transferred to the antibinding region of a single nucleus than to the binding region. It is evident, however, from the shapes of the contours that the charge increase in the binding region is concentrated along the bond axis where it exerts a maximum force of attraction on the nuclei while the buildup in the antibinding region is more diffuse.

   The net forces on the nuclei are zero for each molecule. Therefore, the force exerted by the charge density in the binding region balances not only the force of nuclear repulsion but the force exerted by the charge buildup in the antibinding region as well. The nuclei are in each case bound by the charge increase which is shared equally by both nuclei.

   An important physical property of a molecule is its bond energy, the amount of energy required to break the bond or bonds in a molecule and change it back into its constituent atoms. The bond energies of the second-row homonuclear diatomic molecules increase from either Li₂ or F₂ to a maximum value for the central member of the series, N₂ (Table 7-3).

   We may rationalize the variation in the bond energies and the differences in the bond density maps in terms of the orbital theory of bonding. The simple bonding theory proposed in the preceding chapter equated the valency of an atom to its number of unpaired electrons. Thus the number of electron pair bonds formed between atoms in this series of molecules is predicted to be one for Li₂, B₂ and F₂, two for C₂ and O₂, and three for N₂. Reference to Table 7-3 reveals a parallelism between the bond energy and the number of electron pair bonds present in each molecule.

   The detailed variation in bond energy through the series can be accounted for in terms of the type of bond (whether it is formed for s or p orbitals) present in each molecule, a feature which is clearly reflected in the bond density maps, and even more strikingly portrayed in their profiles (Fig. 7-5).

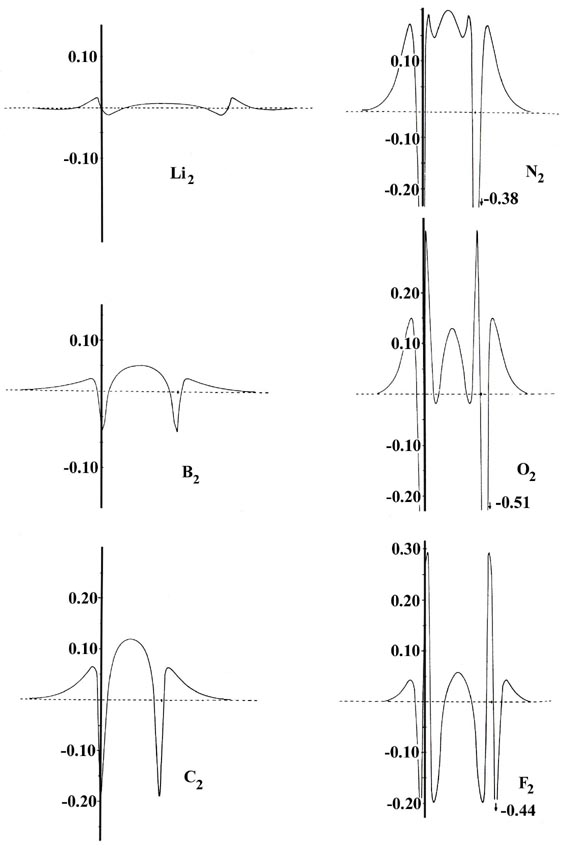
Fig. 7-5.  Profiles of the bond density maps for the homonuclear diatomic molecules.

The bond in Li₂ is formed primarily from the overlap of 2s atomic orbitals on each lithium atom. The 2s atomic density of lithium is a diffuse spherical distribution. These same characteristics are evident in the total charge distribution for Li₂ and particularly in its bond density map. The charge increase in the binding region, while large in amount (Table 7-2),  is very diffuse and the bond density profile shows that relative to the other molecules, the charge increase is not concentrated along the bond axis. These are the very features expected for a bond resulting from the overlap of distorted, nondirectional s orbitals.

  B₂ and F₂ also have but a single pair bond. However, the bonds in these two molecules are formed primarily from the overlap of 2ps orbitals. Since a ps orbital is directed along the bond axis, it is more effective than an s orbital at concentrating charge density along this same axis. This is particularly evident when we compare the profiles of the bond densities for F₂ and B₂ with the profile for Li₂. Similarly, the presence of two electron pair bonds and the still larger bond energies found for C₂ and O₂ are reflected in the larger increases in the charge densities along the internuclear axis in the binding region. Notice that while B₂ concentrates three times as much charge as O₂ in the binding region, it is not concentrated along the bond axis to as great an extent as in O₂, and consequently its bond energy is the smaller of the two.

   The nitrogen molecule possesses three electron pair bonds and the largest bond energy of the molecules in this series. The charge increase in the binding region is concentrated along the bond axis to a far greater extent in this molecule than in any of the other molecules in the series. This concentration of the charge density gives N₂ a stronger bond than C₂ even though the total charge increase in its binding region is only one half as great as that for C₂.

   The comparison of the bond energies in this series of molecules clearly illustrates that the strength of a bond is not simply related to the number of electronic charges in the binding region. As important as the amount of charge is the exact disposition of the charge density in the molecule, whether it is diffuse or concentrated.