An Introduction to the Electronic Structure of Atoms and Molecules

Dr. Richard F.W. Bader 
Professor of Chemistry / McMaster University / Hamilton, Ontario

Preface
1. The Nature of the Problem
  •  Introduction
  •  Some Important Experiments with Electrons and Light
  •  Units of Measurement used in Atomic Physics
  •  Further Reading
  •  Problems
2.  The New Physics
3.  The Hydrogen Atom
4.  Many-Electron Atoms
5.  Electronic Basis for the Properties of the Elements
6.  The Chemical Bond
7.  Ionic and Covalent Binding
8.  Molecular Orbitals
Table of Contour Values
 

Problems
 
1. Atoms or ions in a crystal are arranged in regular arrays as typified by the simple lattice structure shown in Fig. 1-2. 

Fig. 1-2. A two-dimensional display of a simple crystal lattice showing an incoming and a reflected beam of X-rays.

This structure is repeated in the third dimension. X-rays are a form of light with a very short wavelength. Since the spacings between the planes of atoms in a crystal, denoted by d, are of the same order of magnitude of the wavelength of X-rays (~10-8 cm), a beam of  X-rays reflected from the crystal will exhibit interference effects. That is, the layers of atoms in the crystal act as a diffraction grating. The reflected beam of X-rays will be in phase if the difference in the path length followed by waves which strike succeeding layers in the crystal is an integral number of wavelengths. When this occurs the reflected X-rays reinforce one another and produce a beam of high intensity for that particular glancing angle q. For some other values of the angle q, the difference in path lengths will not be equal to an integral number of wavelengths. The reflected waves will then be out of phase and the resulting interference will greatly decrease the intensity of the reflected beam. The difference in path length traversed by waves reflected by adjacent layers is 2dsinq as indicated in the diagram. Therefore,
(6)
 
which states that the reflected beam will be intense at those angles for which the difference in path length is equal to a whole number of wavelengths. Thus a diffraction pattern is produced, the intensity of the reflected X-ray beam varying with the glancing angle q.
(a) By using X-rays with a known wavelength and observing the angles of maximum intensity for the reflected beam, the spacings between the atoms in a crystal, the quantity d in equation (6), may be determined. For example, X-rays with a wavelength of 1.5420 C produce an intense first-order (n =  1 in equation (6)) reflection at an angle of 21.01° when scattered from a crystal of nickel. Determine the spacings between the planes of nickel atoms.
(b) Remarkably, electrons exhibit the same kind of diffraction pattern as do X-rays when reflected from a crystal; this provides a verification of de Broglie's prediction. The experiment performed by Davisson and Germer employed low energy electrons which do not penetrate the crystal.  (High energy electrons do.)  In their experiment the diffraction of the electrons was caused by the nickel atoms in the surface of the crystal. A beam of electrons with an energy of 54 ev was directed at right angles to a surface of a nickel crystal with d = 2.15 C. Many electrons are reflected back, but an intense sharp reflected beam was observed at an angle of 50° with respect to the incident beam. 

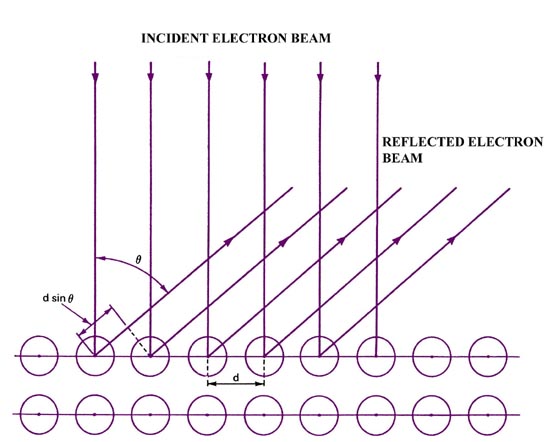
Fig. 1-3. The classic experiment of Davisson and Germer: the scattering of low energy electrons from the surface of a nickel crystal.

As indicated in Fig. 1-3 the condition for reinforcement using a plane reflection grating is
(7)
 
using equation (7) with n = 1 for the intense first-order peak. Observed at 50°, calculate the wavelength of the electrons. Compare this experimental value for l with that calculated using de Broglie's relationship.
(8)
 
The momentum mu may be calculated from the kinetic energy of the electrons using equation (5) in the website.
(c) Even neutrons and atoms will exhibit diffraction effects when scattered from a crystal. In 1994 Professor Brockhouse of McMaster University shared the Nobel prize in physics with Professor Shull of MIT for their work on the scattering of neutrons by solids and liquids. Professor Brockhouse demonstrated how the inelastic scattering of neutrons can be used to gain information about the motions of atoms in solids and liquids. Calculate the velocity of neutrons which will produce a first-order reflection for q = 30° for a crystal with d = 1.5 ´ 10-8 cm. Neutrons penetrate a crystal and hence equation (6) should be used to determine l. The mass of the neutron is 1.66 ´ 10-24 g.
(d) The neutrons obtained from an atomic reactor have high velocities. They may be slowed down by allowing them to come into thermal  equilibrium with a cold material. This is usually done by passing them through a block of carbon. The kinetic theory relationship between average kinetic energy and the absolute temperature, 
 
may be applied to the neutrons. Calculate the temperature of the carbon block which will produce an abundant supply of neutrons with velocities in the range required for the experiment described in (c).