An Introduction to the Electronic Structure of Atoms
and Molecules
Dr. Richard F.W. Bader
Professor of Chemistry / McMaster University / Hamilton,
Ontario
|
The Relative Binding Ability of Molecular Orbitals
We may determine the relative importance of each orbital density in
the overall binding of the nuclei in a molecule through a comparison of
the forces which the various molecular orbital charge distributions exert
on the nuclei. In molecular orbital theory, the total charge density is
given by the sum of the orbital charge densities. Thus the total force
exerted on the nuclei by the electronic charge distribution will be equal
to the sum of the forces exerted by the charge density in each of the molecular
orbitals. It is of interest to compare the effectiveness of each orbital
charge density in binding the nuclei with some standard case in which they
all exhibit the same ability. The limiting forms of the molecular orbitals
for the case of the separated atoms have this desired property. In addition,
the properties of the separated atoms form a useful basis for the discussion
of any molecular property from the point of view of determining the changes
which have been brought about by the formation of the chemical bond.
Suppose we label the two nuclei of a homonuclear diatomic
molecule as A and B and consider the forces exerted on the A nucleus by
the pair of electrons in a molecular orbital when the orbital has assumed
its limiting form for the separated atoms. At this limit, one electron
correlates with an atomic orbital on nucleus A and the other with
an identical orbital on nucleus B. The discussion of the forces exerted
on the nuclei by such a limiting charge distribution is similar to the
discussion given previously in Section 6 for the case of two separated
hydrogen atoms. The charge density in the orbital on the A nucleus will
not exert a force on that nucleus since an undistorted atomic orbital is
centrosymmetric with respect to its nucleus. The charge density of the
electron which correlates with the B nucleus will exert a force on the
A nucleus equivalent to that obtained by concentrating the charge density
to a point at the position of the B nucleus. The electron which correlates
with the B nucleus will screen one of the nuclear charges of B from the
A nucleus. Thus the force exerted on one of the nuclei by the pair of electrons
in a molecular orbital for the limiting state of the separated atoms is
equivalent to that obtained by placing one negative charge at the position
of the second nucleus. Of the pair of electrons in a given homonuclear
molecular orbital, only one is effective in binding either nucleus in the
limit of the separated atoms.
If there are a total of N electrons in the molecule,
there will be N/2 occupied molecular orbitals since each molecular
orbital contains a pair of electrons. Therefore, a total of N/2
electrons will correlate with each nucleus. The molecule dissociates into
two neutral atoms each with a nuclear charge Z = N/2. Thus the N/2
electrons which correlate with each nucleus will exactly cancel the nuclear
charge of both nuclei; the final force on the nuclei will be zero.
The limiting force exerted on the A nucleus by the pair
of electrons in a molecular orbital is (ZAe2/R2)(-1),
that is, the force is equivalent to placing one negative charge at
the position of the B nucleus. Thus we may express the total limiting
force on nucleus A as the product of (ZAe2/R2)
with the difference between the number of positive charges on the B nucleus
(ZB) and the number of electronic charges which
are effective in exerting a force on the A nucleus, (N/2):
The quantity N/2 is the charge equivalent of the
electronic force, the number of charges which when placed at the position
of one nucleus exerts the same force on the second nucleus as does the
actual charge distribution. The zero force between the separated atoms
may be viewed as a result of each electron screening one nuclear charge
on one nucleus from the nuclear charge of the other atom.
As the atoms approach one another to form a chemical bond,
the atomic distributions on each atom become increasingly distorted and
charge density is transferred to the binding region between the nuclei.
There is a net force of attraction on the nuclei. We may again express
the electronic force on the A nucleus in terms of its charge equivalent
by multiplying the electronic force of attraction by R2/ZAe2.
Because of the distortion of the atomic orbital densities and the formation
of molecular orbitals concentrating charge density in the region between
the nuclei, the charge density of more than just one electron in each molecular
orbital is effective in binding the nuclei. Thus at intermediate R
values the charge equivalent of the electronic force exceeds its limiting
value of N/2 required to screen the nuclear charge and the result
is a force of attraction drawing the nuclei together.
When the distance between the nuclei is further decreased
to its equilibrium value the force on the nuclei is again equal to zero.
At this point, as when R equals infinity, the charge equivalent
of the electronic force equals the nuclear charge. However, the state of
electrostatic equilibrium in the molecule does not correspond to the charge
density in each molecular orbital effectively screening one nuclear charge
as it did in the separated atoms. Instead the charge equivalent of the
density in each molecular orbital may be less than, equal to, or greater
than the limiting value of unity observed for the separated atoms.
An orbital which concentrates charge density in the binding
region will exert a force on the nuclei with a charge equivalent greater
than unity. Such an orbital is called binding as it does
more than simply screen one unit of positive charge on each nucleus. The
charge equivalent of an orbital which concentrates density in the antibinding
regions will be less than the separated atom value of unity. Such an orbital
is termed antibinding as the charge density does not screen
one unit of positive charge on each nucleus. When the charge equivalent
of the force equals unity, it implies that the orbital charge density plays
the same role in the molecule as in the separated atoms, that of screening
one nuclear charge on B from nucleus A. An orbital with this property is
termed nonbinding.
Thus, by comparing the charge equivalent of the force exerted
by the density in each molecular orbital with its separated atom value
of unity, we may classify the orbitals as binding, antibinding or nonbinding:
| Binding orbital |
|
charge equivalent > unity |
| Nonbinding orbital |
|
charge equivalent ~ unity |
| Antibinding orbital |
|
charge equivalent < unity |
Table 8-1.
Charge Equivalents of the Orbital Forces in Homonuclear Diatomic Molecules
|
Molecule
|
1sg
|
1su
|
2sg
|
2su
|
1pu
|
3sg
|
1pg
|
Sum = ZB
|
Re (au)
|
|
He2
|
1.78
|
-0.42
|
|
|
|
|
|
1.36*
|
(1.750)*
|
|
Li2
|
0.70
|
0.68
|
1.62
|
|
|
|
|
3.00
|
5.051
|
|
Be2
|
1.05
|
1.08
|
2.00
|
-0.40
|
|
|
|
3.68*
|
(3.500)*
|
|
B2
|
0.98
|
0.98
|
2.32
|
-0.48
|
1.20
|
|
|
5.00
|
3.005
|
|
C2
|
0.97
|
0.95
|
2.25
|
-0.43
|
1.13
|
|
|
6.00
|
2.348
|
|
N2
|
1.15
|
1.08
|
2.67
|
-0.47
|
1.21
|
0.15
|
|
7.00
|
2.068
|
|
O2
|
1.23
|
1.14
|
2.94
|
-0.52
|
1.30
|
0.18
|
0.43
|
8.00
|
2.282
|
|
F2
|
1.24
|
1.12
|
2.45
|
-0.16
|
1.24
|
0.52
|
0.67
|
9.00
|
2.680
|
*He2 and Be2
form only weakly bound van der Waals molecules for relatively large internuclear
seperations. The values of R quoted for these molecules are the
internuclear distances used in the calculation of the charge equivalents
listed in the table.
All of the values are quoted for double occupation of the orbitals
for comparative purposes. The values marked by are to be doubled to obtain
the total electronic force as they refer to filled
p
orbitals.
The charge equivalents of the orbital forces for some homonuclear diatomic
molecules are given in Table 8-1. Except for He2
and Be2 the sum of the charge equivalents
equals the nuclear charge in each case as required for electrostatic equilibrium
and the formation of a stable molecule. The charge equivalents of the orbital
forces provide a quantitative measure of the role each orbital density
plays in the binding of the nuclei in the molecule.
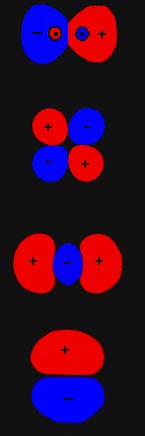
The 1sg orbital
in He2 is binding. Of the two electronic
charges in the 1sg orbital,
1.78 of them are effective in binding the nuclei when R = 1.75 ao
as opposed to the one electronic charge which exerts a force when R
= ¥. The 1su
charge density, however, is strongly antibinding. The transfer of charge
density to the antibinding regions in the formation of the 1su
orbital in He2 is so great that the charge
equivalent is negative in sign. The antibinding nature of this orbital
is very evident in the form of its charge distribution (Fig.
8-6). Not only does the charge density in this orbital no longer screen
a positive charge on one nucleus from the other, it actually exerts a repulsive
force on the nuclei, one which pulls the nuclei further apart from one
another. The total eletronic force exerted on a nucleus in He2
at R = 1.75 ao is equivalent to placing (1.78
- 0.42) = 1.36 negative charges at the position of the second nucleus.
Since the nuclear charge on helium is 2.00, a total of (2.00 - 1.36) =
0.64 positive charges on the second nucleus are left unscreened by the
charge density. The net force on the nuclei is thus a repulsive one.
The 1sg and
1su molecular orbitals are
inner shell orbitals in the remaining molecules, Li2
to
F2. An idealized inner shell molecular
orbital has a charge equivalent of unity, the same as the separated atom
value. Each electron should be localized in an atomic-like distribution
and screen one nuclear charge. This is illustrated by the 1sg
and 1su charge density maps
for the O2 molecule (Fig.
8-8). The charge equivalents of the 1sg
and 1su orbital densities
for Li2 (Fig.
8-7) are significantly less than unity. While these orbitals are not
as contracted around the nuclei in Li2
as they are in O2 (the nuclear charge for
lithium is three compared to eight for oxygen), they are still atomic-like
with no effective overlap between the two centres. The charge equivalents
are less than the screening value of unity because each of the atomic-like
distributions is polarized into the antibinding region and exerts an antibinding
force on the nucleus on which it is centred. The charge equivalents for
the 1sg and 1su
density distributions in the remaining molecules are close to unity indicating
that they are essentially nonbinding inner shell orbitals. The slight binding
character of the 1sg charge
density in O2 and F2
is the result of small inward polarizations of the atomic-like distributions.
The 2sg molecular
charge density is binding in every molecule. A comparison of the charge
equivalents shows that the 2sg
charge density is the most binding of all the molecular orbitals in this
series of molecules. The charge equivalent of the force exerted by the
2sg density in O2
is almost three times greater than it is for the separated oxygen atoms.
This is a result of the large amount of charge density accumulated in the
binding region by this orbital (Fig. 8-8).
The 2su orbital
is uniformly strongly antibinding. The extreme concentration of charge
density in the antibinding regions observed for the 2su
orbital is typified by the 2su
density plot for O2 (Fig.
8-8). It is obvious that the density in this orbital, as that in the
1su orbital of He2
will pull the nuclei away from one another rather than bind them together.
Notice that Be2 is analogous to He2
except that the 2sg and 2su
orbitals rather than the 1sgand
1su orbital densities are
involved. In Be2 the 1sg
and 1su densities are nonbinding
and together simply screen two nuclear charges on each atom. The 2sg
density exerts a binding force equivalent to one electronic charge in excess
of the simple screening effect. The 2su
orbital density, however, leaves a single nuclear charge unscreened which
cancels the net attractive force of the 2sg
density
and in addition exerts an antibinding force equivalent to increasing the
nuclear charge by 0.40 units. The beryllium molecule is therefore unstable
at this value of R.
The 1pu orbital
density is binding in each case, but only weakly so. The charge density
of a pu molecular orbital
is concentrated around the internuclear axis rather than along it as in
a sg molecular orbital. Consequently
the 1pu density distributions
exert only weak binding forces on the nuclei. In fact, the inner shell
1sg charge density in F2
exerts as large a binding force on the nuclei as does a pair of electrons
in the1pu orbital.
The charge equivalent of the 3sg
orbital
density is less than unity in the three cases where it is occupied. Thus
it is an antibinding orbital even though it is of sg
symmetry. The charge density contours for this orbital in O2
(Fig. 8-8) show that charge
density is accumulated in the region between the nuclei as expected for
an orbital of sg symmetry.
However, the 3sg orbital correlates
with a 2ps atomic orbital on each nucleus.
The strong participation of the 2ps orbitals
in the molecular orbital is evidenced by the node at each nucleus and by
the concentration of charge density on both sides of each nucleus. The
concentration of charge in the antibinding regions nullifies the binding
effect arising from the accumulation of charge density in the region between
the nuclei. The net result is an attractive force considerably less than
that required to screen one positive charge on each nucleus.
The 1pg orbital
density is only weakly antibinding just as the 1pu
density is only weakly binding. The formation of the 1pg
orbital results in the removal of charge density from the binding region,
not from along the internuclear axis but instead from regions around the
axis. Notice that unlike the 2su
orbital densities, the 1pg charge
density is antibinding only in the sense that it does not screen its share
of nuclear charge, not because it exerts a force which draws the nuclei
apart.