An Introduction to the Electronic Structure of Atoms and Molecules

The concept of a molecular orbital is readily extended to provide a description of the electronic structure of a polyatomic molecule. Indeed molecular orbital theory forms the basis for most of the quantitative theoretical investigations of the properties of large molecules.

   In general a molecular orbital in a polyatomic system extends over all the nuclei in a molecule and it is essential, if we are to understand and predict the spatial properties of the orbitals, that we make use of the symmetry properties possessed by the nuclear framework. An analysis of the molecular orbitals for the water molecule provides a good introduction to the way in which the symmetry of a molecule determines the forms of the molecular orbitals in a polyatomic system.

   There are three symmetry operations which transform the nuclear framework of the water molecule into itself and hence leave the nuclear potential field in which the electrons move unchanged (Fig. 8-10).

Fig. 8-10.  Symmetry elements for H₂O. The bottom two diagrams illustrate the transformations of the 2p_y orbital on oxygen under the C₂ and s₂ symmetry operations.

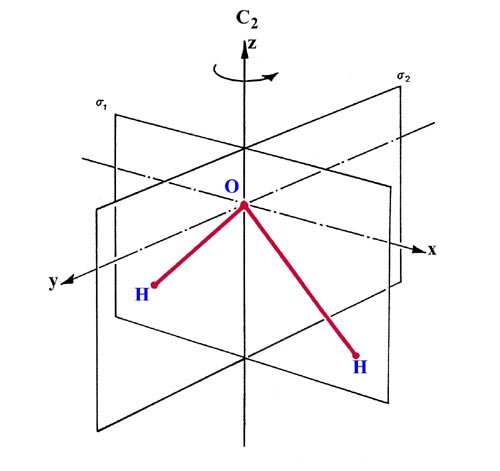
For each symmetry operation there is a corresponding symmetry element. The symmetry elements for the water molecule are a two-fold axis of rotation C₂ and two planes of symmetry s₁ and s₂ (Fig. 8-10). A rotation of 180° about the C₂ axis leaves the oxygen nucleus unchanged and interchanges the two hydrogen nuclei. A reflection through the plane labelled s₁ leaves all the nuclear positions unchanged while a reflection through s₂ interchanges the two protons. The symmetry operations associated with the three symmetry elements either leave the nuclear positions unchanged or interchange symmetrically equivalent (and hence indistinguishable) nuclei. Every molecular orbital for the water molecule must, under the same symmetry operations, be left unchanged or undergo a change in sign.

   Similarly we may use the symmetry transformation properties of the atomic orbitals on oxygen and hydrogen together with their relative orbital energy values to determine the primary atomic components of each molecular orbital in a simple LCAO approximation to the exact molecular orbitals. Only atomic orbitals which transform in the same way under the symmetry operations may be combined to form a molecular orbital of a given symmetry. The symmetry transformation properties of the atomic orbitals on oxygen and hydrogen are given in Table 8-3. A value of +1 or -1 opposite a given orbital in the table indicates that the orbital is unchanged or changed in sign respectively by a particular symmetry operation.

   The 1s, 2s and 2p_z orbitals of oxygen are symmetric (i.e., unchanged) with respect to all three symmetry operations. They are given the symmetry classification a₁. The 2p_x orbital, since it possesses a node in the s₂ plane (and hence is of different sign on each side of the plane) changes sign when reflected through the s₂ plane or when rotated by 180° about the C₂ axis. It is classified as a b₂ orbital. The 2p_y orbital is antisymmetric with respect to the rotation operator and to a reflection through the s₁ plane. It is labelled b₁.

   The hydrogen 1s orbitals when considered separately are neither unchanged nor changed in sign by the rotation operator or by a reflection through the s₂ plane. Instead both these operations interchange these orbitals. The hydrogen orbitals are said to be symmetrically equivalent and when considered individually they do not reflect the symmetry properties of the molecule. However, the two linear combinations  (1s₁ + 1s₂)  and  (1s₁ - 1s₂) do behave in the required manner. The former is symmetric
under all three operations and is of a₁ symmetry while the latter is antisymmetric with respect to the rotation operator and to a reflection through the plane s₂ and is of b₂ symmetry.

   The molecular orbitals in the water molecule are classified as a₁, b₁ or b₂ orbitals, as determined by their symmetry properties. This labelling of the orbitals is analogous to the use of the s-p and g-u classification in linear molecules. In addition to the symmetry properties of the atomic orbitals we must consider their relative energies to determine which orbitals will overlap significantly and form delocalized molecular orbitals.

   The 1s atomic orbital on oxygen possesses a much lower energy than any of the other orbitals of a₁ symmetry and should not interact significantly with them. The molecular orbital of lowest energy in H₂O should therefore correspond to an inner shell 1s atomic-like orbital centred on the oxygen. This is the first orbital of a₁ symmetry and it is labelled la₁. Reference to the forms of the charge density contours for the la, molecular orbital (Fig. 8-11) substantiates the above remarks regarding the properties of this orbital.

Fig. 8-11.  Contour maps of the molecular orbital charge densities for H₂O. The maps for the la₁, 2a₁, 3a₁and 1b₂ orbitals (all doubly-occupied) are shown in the plane of the nuclei. The lb₁ orbital has a node in this plane and hence the contour map for the 1b₁ orbital is shown in the plane perpendicular to the molecular plane. The total molecular charge density for H₂O is also illustrated. The density distributions were calculated from the wave function determined by R. M. Pitzer, S. Aung and S. I. Chan, J. Chem. Phys. 49, 2071 (1968). Click here for contour values.

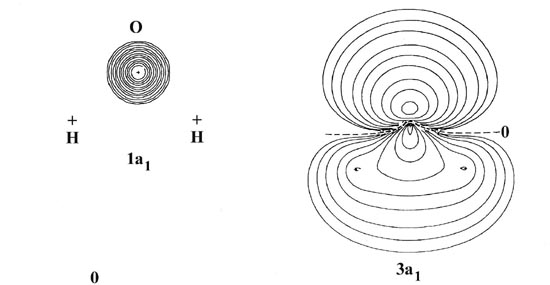
Notice that the orbital energy of the la₁ molecular orbital is very similar to that for the 1s atomic orbital on oxygen. The 1a₁ orbital in H₂O is, therefore, similar to the ls inner shell molecular orbitals of the diatomic hydrides.

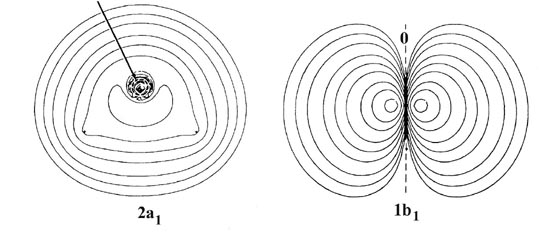
   The atomic orbital of next lowest energy in this system is the 2s orbital of a₁ symmetry on oxygen. We might anticipate that the extent to which this orbital will overlap with the (1s₁ + 1s₂) combination of orbitals on the hydrogen atoms to form the 2a₁ molecular orbital will be intermediate between that found for the 2s molecular orbitals in the diatomic hydrides CH and HF (Fig. 8-9). The 2s orbital in CH results from a strong mixing of the 2s orbital on carbon and the hydrogen 1s orbital. In HF the participation of the hydrogen orbital in the 2s orbital is greatly reduced, a result of the lower energy of the 2s atomic orbital on fluorine as compared to that of the 2s orbital on carbon.

   Aside from the presence of the second proton, the general form and nodal structure of the 2a₁ density distribution in the water molecule is remarkably similar to the 2s distributions in CH and HF, and particularly to the latter. The charge density accumulated on the bonded side of the oxygen nucleus in the 2a₁ orbital is localized near this nucleus as the corresponding charge increase in the 2s orbital of HF is localized near the fluorine. The charge density of the 2a₁ molecular orbital accumulated in the region between the three nuclei will exert a force drawing all three nuclei together. The 2a₁ orbital is a binding orbital.

   Although the three 2p atomic orbitals are degenerate in the oxygen atom the presence of the two protons results in each 2p orbital experiencing a different potential field in the water molecule. The nonequivalence of the 2p orbitals in the water molecule is evidenced by all three possessing different symmetry properties. The three 2p orbitals will interact to different extents with the protons and their energies will differ.

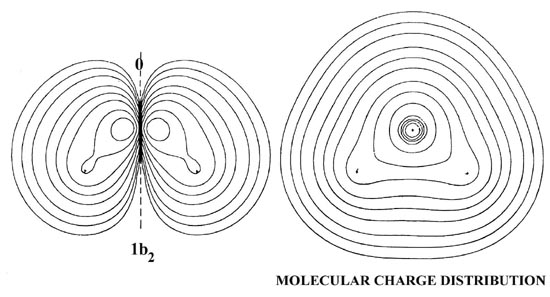
   The 2p_x  orbital interacts most strongly with the protons and forms an orbital of b₂ symmetry by overlapping with the (1s₁ - 1s₂) combination of 1s orbitals on the hydrogens. The charge density contours for the lb₂ orbital indicate that this simple LCAO description accounts for the principal  features of this molecular orbital. The lb₂ orbital concentrates charge density along each O-H bond axis and draws the nuclei together. The charge density of the 1b₂ orbital binds all three nuclei. In terms of the forces exerted on the nuclei the 2a₁ and lb₂ molecular orbitals are about equally effective in binding the protons in the water molecule.

    The 2p_z orbital may also overlap with the hydrogen 1s orbitals, the (1s₁ + 1s₂) a₁ combination, and the result is the 3a₁ molecular orbital. This orbital is concentrated along the z-axis and charge density is accumulated in both the bonded and nonbonded sides of the oxygen nucleus. It exerts a binding force on the protons and an antibinding force on the oxygen nucleus, a behaviour similar to that noted before for the 3s orbitals in CH and HF.

    The 2p_y orbital is not of the correct symmetry to overlap with the hydrogen 1s orbitals. To a first approximation the 1b₁ molecular orbital will be simply a 2p_y atomic orbital on the oxygen, perpendicular to the plane of the molecule. Reference to Fig. 8-11 indicates that the 1b₁ orbital does resemble a 2p atomic orbital on oxygen but one which is polarized into the molecule by the field of the protons. The 1b₁ molecular orbital of H₂O thus resembles a single component of the 1p molecular orbitals of the diatomic hydrides. The 1b₁ and the 1p orbitals are essentially nonbinding. They exert a small binding force on the heavy nuclei because of the slight polarization. The force exerted on the protons by the pair of electrons in the 1b₁ orbital is slightly less than that required to balance the force of repulsion exerted by two of the nuclear charges on the oxygen nucleus. The 1b₁ and 1p electrons basically do no more than partially screen nuclear charge on the heavy nuclei from the protons.

   In summary, the electronic configuration of the water molecule as determined by molecular orbital theory is

   Before closing this introductory account of molecular orbital theory, brief mention should be made of the very particular success which the application of this theory has had in the understanding of the chemistry of a class of organic molecules called conjugated systems. Conjugated molecules are planar organic molecules consisting of a framework of carbon atoms joined in chains or rings by alternating single and double bonds. Some examples are

In the structural formulae for the cyclic molecules, e.g., benzene and naphthalene, it is usual not to label the positions of the carbon and hydrogen atoms by their symbols. A carbon atom joined to just two other carbon atoms is in addition bonded to a hydrogen atom, the C—H bond axis being projected out of the ring in the plane of the carbon framework and bisecting
the CCC bond angle.

   The notion of these molecules possessing alternating single and double bonds is a result of our attempt to describe the bonding in terms of conventional chemical structures. In reality all six C—C bonds in benzene are identical and the C—C bonds in the other two examples possess properties intermediate between those for single and double bonds. In other words, the pairs of electrons forming the second or p bonds are not localized between specific carbon atoms but are delocalized over the whole network of carbon atoms, a situation ideally suited for a molecular orbital description.

   We may consider each carbon atom in a conjugated molecule to be sp² hybridized and bonded through these hybrid orbitals to three other atoms in the plane. This accounts for the bonding of the hydrogens and for the formation of the singly-bonded carbon network. The electrons forming these bonds are called s electrons. The axis of the remaining 2p orbital on each carbon atom is directed perpendicular to the plane of the molecule and contains a single electron, called a p electron. A simple adaptation of molecular orbital theory, called Hückel theory, which takes the s bonds for granted and approximates the molecular orbitals of the p electrons in terms of linear combinations of the 2pp atomic orbitals on each carbon atom, provides a remarkably good explanation of the properties of conjugated molecules. Hückel molecular orbital theory and its applications are treated in a number of books, some of which are referred to at the end of this chapter.