An Introduction to the Electronic Structure of Atoms and Molecules

    In quantum mechanics, Newton's familiar equations of motion are replaced by Schrödinger's equation. We shall not discuss this equation in any detail, nor indeed even write it down, but one important aspect of it must be mentioned. When Newton's laws of motion are applied to a system, we obtain both the energy and an equation of motion. The equation of motion allows us to calculate the position or coordinates of the system at any instant of time. However, when Schrödinger's equation is solved for a given system we obtain the energy directly, but not the probability distribution functionCthe function which contains the information regarding the position of the particle. Instead, the solution of Schrödinger's equation gives only the amplitude of the probability distribution function along with the energy. The probability distribution itself is obtained by squaring the probability amplitude. (Click here for note.) Thus for every allowed value of the energy, we obtain one or more (the energy value may be degenerate) probability amplitudes.

    The probability amplitudes are functions only of the positional coordinates of the system and are generally denoted by the Greek letter y (psi). For a bound system the amplitudes as well as the energies are determined by one or more quantum numbers. Thus for every E_n we have one or more y_n's and by squaring the  y_n's we may obtain the corresponding P_n's.

 Let us look at the forms of the amplitude functions for the simple system of an electron confined to motion on a line. For any system, y  is simply some mathematical function of the positional coordinates. In the present problem which involves only a single coordinate x, the amplitude functions may be plotted versus the x-coordinate in the form of a graph. The functions y_n are particularly simple in this case as they are sin functions.
  The first few y_n's are shown plotted in Fig. 2-8.

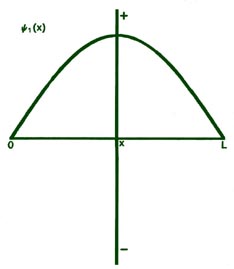
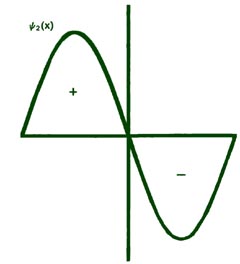
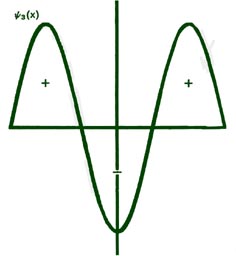
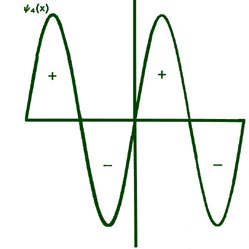
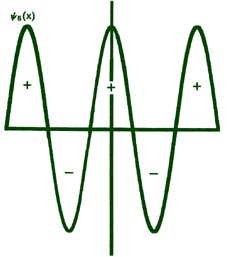
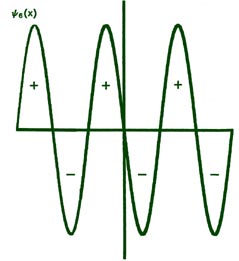
Fig. 2-8. The first six probability amplitudes y_n(x) for an electron moving on a line of length L. Note the y_n(x) may be negative in sign for certain values of x. The y_n(x) are squared to obtain the probability distrubrition functions P_n(x), which are, therefore, positive for all values of x. Wherever y_n(x) crosses the x-axis and changes sign, a node appears in the corresponding P_n(x).

Each of these graphs, when squared, yields the corresponding P_n curves shown previously. When n = 1,
  When x = 0,
  When x = L,
  When x = L/2,
  Thus y equals zero at x = 0 and x = L and is a maximum when x = L/2. When this function is squared, we obtain:
  and the graph (Fig. 2-4) previously given for P₁(x).

    As illustrated previously in Fig. 2-4, the value of y_n²(x) or P_n(x) multiplied by Dx, y_n²(x)Dx, or P_n(x)Dx, is the probability that the electron will be found in some particular small segment of the line Dx. The constant factor of  which appears in every y_n(x) is to assure that when the value of  y_n²(x)Dx is summed over each of the small segments Dx, the final value will equal unity. This implies that the probability that the electron is somewhere on the line is unity, i.e., a certainty. Thus the probability that the electron is in any one of the small segments Dx (the value of  y_n²(x)Dx or P_n(x)Dx evaluated at a value of x between 0 and L) is a fraction of unity, i.e., a probability less than one. (Click here for note.)

   Each y_n  must necessarily go to zero at each end of the line, since the probability of the electron not being on the line is zero. This is a physical condition which places a mathematical restraint on the y_n . Thus the only acceptable y_n 's are those which go to zero at each end of the line. A solution of the form shown in Fig. 2-9 is, therefore, not an acceptable one. Since there is but a single value of the energy for each of the possible y_n functions, it is clear that only certain discrete values of the energy will be allowed. The physical restraint of confining the motion to a finite length of line results in the quantization of the energy. Indeed, if the line is made infinitely long (the electron is then free and no longer bound), solutions for any value of n, integer or non-integer, are possible; correspondingly, all energies are permissible. Thus only the energies of bound systems are quantized.

Fig. 2-9. An unacceptable form for yn(x).

   The y_n 's have the appearance of a wave in that a given value of y_n(x) is repeated as x is increased. They are periodic functions of x. We may, if we wish, refer to the wavelength of y_n. The wavelength of  y₁ is 2L since only one half of a wave fits on the length L. The wavelength for y₂, is L since one complete wave fits in the length L. Similarly l₃, = (2/3)L and l₄ = (2/4)L. In general:
  Because of the wave-like nature of the y_n 's , the new physics is sometimes referred to as wave mechanics, and the y_n  functions are called wave functions. However, it must be stressed that a wave function itself has no physical reality. All physical properties are determined by the product of the wave function with itself. It is the product y_n(x)y_n(x) which yields the physically measurable probability distribution. Thus y_n² may be observed but not y_n itself.

    A y_n does not represent the trajectory or path followed by an electron in space. We have seen that the most we can say about the position of an electron is given by the probability function y_n². We do, however, refer to the wavelengths of electrons, neutrons, etc. But we must remember that the wavelengths refer only to a property of the amplitude functions and not to the motion of the particle itself.

    A number of interesting properties can be related to the idea of the wavelengths associated with the wave functions or probability amplitude functions. The wavelengths for our simple system are given by l = 2L/n. Can we identify these wavelengths with the wavelengths which de Broglie postulated for matter waves and which obeyed the relationship:
  The absolute value for the momentum (the magnitude of the momentum independent of its direction) of an electron on the line is nh/2L. Substituting this into de Broglie's relationship gives:
  So indeed the wavelengths postulated by de Broglie to be associated with the motions of particles are in reality the wavelengths of the probability amplitudes or wave functions. There is no need to postulate "matter waves" and the results of the electron diffraction experiment of Davisson and Germer for example can be interpreted entirely in terms of probabilities rather than in terms of "matter waves" with a wavelength  l = h/p.

   It is clear that as n increases, l becomes much less than L. For n =  100, y₁₀₀and P₁₀₀ would appear as in Fig. 2-10. When L>>l_n, the nodes in P_n are so close together that the function appears to be a continuous function of x. No experiment could in fact detect nodes which are so closely spaced, and any observation of the position of the electron would yield a result for P₁₀₀ similar to that obtained in the classical case. This is a general result. When l is smaller than the important physical dimensions of the system, quantum effects disappear and the system behaves in a classical fashion. This will always be true when the system possesses a large amount of energy, i.e, a high n value. When, however, l is comparable to the physical dimensions of the system, quantum effects predominate.

Fig. 2-10. The wave function and probability distribution for n = 100.

    Let us check to see whether or not quantum effects will be evident for electrons bound to nuclei to form atoms. A typical velocity of an electron bound to an atom is of the order of magnitude of 10⁹ cm/sec. Thus:
  This is a short wavelength, but it is of the same order of magnitude as an atomic diameter. Electrons bound to atoms will definitely exhibit quantum effects because the wavelength which determines their probability amplitude is of the same size as the important physical dimensionCthe diameter of the atom.

   We can also determine the wavelength associated with the motion of the mass of 1 g moving on a line 1 m in length with a velocity of, say, 1 cm/sec:
  This is an incredibly short wavelength, not only relative to the length of the line but absolutely as well. No experiment could detect the physical implications of such a short wavelength. It is indeed many, many times smaller than the diameter of the mass itself. For example, to observe a diffraction effect for such particles the spacings in the grating must be of the order of magnitude of 1 ´ 10^-27 cm. Such a grating cannot be made from ordinary matter since atoms themselves are about 10¹⁹ times larger than this. Even if such a grating could be found, it certainly wouldn't affect the motion of a mass of 1 g as the size of the mass is approximately 10²⁸ times larger than the spacings in the grating! Clearly, quantum effects will not be observed for massive particles. It is also clear that the factor which determines when quantum effects will be observed and when they will be absent is the magnitude of Planck's constant h. The very small magnitude of h restricts the observation of quantum effects to the realm of small masses.