An Introduction to the Electronic Structure of Atoms and Molecules

    We may use an extension of our simple system to illustrate another important quantum mechanical result regarding energy levels. Suppose we allow the electron to move on the x-y plane rather than just along the x-axis. The motions along the x and y directions will be independent of one another and the total energy of the system will be given by the sum of the energy quantum for the motion along the x-axis plus the energy quantum for motion along the y-axis. Two quantum numbers will now be necessary, one to indicate the amount of energy along each coordinate. We shall label these as n_x and n_y. Let us assume that the motion is confined to a length L along each axis, then:
  Nothing new is encountered when the electron is in the lowest quantum level for which n_x = n_y = 1. The energy E_1,1 simply equals 2h²/8mL².

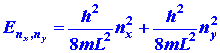
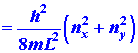Since two dimensions (x and y) are now required to specify the position of the electron, the probability distribution P_1,1(x,y) must be plotted in the third dimension. We may, however, still display P_1,1(x,y) in a two-dimensional diagram in the form of a contour map (Fig. 2-7). All points in the x-y plane having the same value for the probability distribution P_1,1(x,y) are joined by a line, a contour line. The values of the contours increase from the outermost to the innermost, and the electron, when in the level n_x = n_y = 1, is therefore most likely to be found in the central region of the x-y plane.

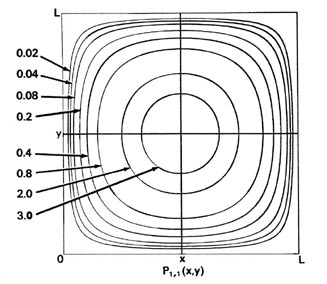
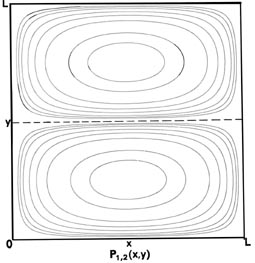
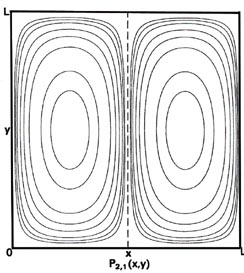
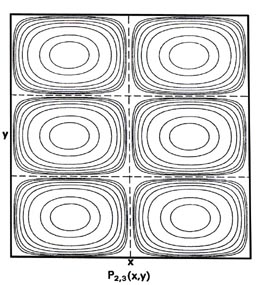
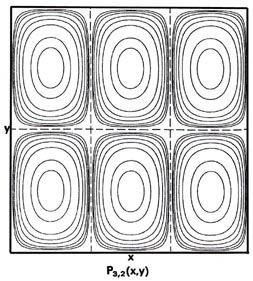
Fig. 2-7.  Contour maps of the probability distributions P_{nx, ny} (x,y) for an electron moving on the x-y plane. The dashed lines represent the postion of nodes, lines along which the probability is zero. P_1,2 (x,y) and P_2,1 (x,y) are distributions for one doubly-degenerate level; P_2,3 (x,y) and P_3,2 (x,y) are examples of distributions for another degenerate level of still higher energy. The same contours are shown in each diagram and their values (in units of 4/L²) are indicated in the diagram for P_1,1(x,y).

A plot of P_1,1(x,y) along either of the axes indicated in Fig. 2-7 (one parallel to the x-axis at y = L/2 and the other parallel to the y-axis at x = L/2) is similar in appearance to that for P₁(x) shown in Fig. 2-4. That is, for a fixed value of y, the contribution to P_1,1(x,y) from the motion along the y-axis is constant and
  Thus, aside from the constant factor, P₁(x) provides a profile, or if P_1,1(x,y) were displayed in three dimensions, a cross section of the contour map of P_1,1(x). A contour map is a display of the probability or density distribution in a plane; a profile is a display of the density distribution along a line.

Now consider the possibility of n_x = 1 and n_y = 2. Then
  We could also have the situation in which n_x = 2 and n_y = 1. This does not change the value of the total energy,
  but the probability distributions (Fig. 2-7) are different, P_1,1(x,y) ¹P_2,1 (x,y). When n_x = 1 and n_y = 2, there must be a node on the y-axis, i.e., a zero probability of finding the electron at y = L/2. Thus a slice through P_1,2(x y) at x = L/2 parallel to the y-axis must be similar to the figure for P₂(x), while a slice parallel to the x-axis will still be similar to P₁(x). Just the reverse is true for the case n_x = 2 and n_y = 1. In this case, whether or not we can distinguish experimentally between the x- and y-axes, there are two different arrangements for the distribution of the electron, both of which have the same energy. The energy level is said to be degenerate. The degeneracy of an energy level is equal to the number of distinct probability distribution for the system, all of which belong to this same energy level.

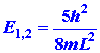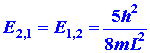The concept of degeneracy in an energy level has important consequences in our study of the electronic structure of atoms.